Basics of RF coil development for MRI

[Leonid92]

TL;DR

Basics of RF coil development for MRI

Hi all,

I'm trying to understand basics of radiofrequency (RF) coil development for magnetic resonance imaging (MRI).
For example, the problem is to develop simple surface single-loop RF coil tuned to 100 MHz.
In program Coil32, I set the following parameters:
diameter of the loop D = 20 mm;
wire diameter d = 2 mm;
working frequency = 100 MHz;
material of wire = copper.
The program calculates inductance of one turn loop coil and coil constructive Q-factor:
inductance = 0.033 uH (microhenries);
coil constructive Q-factor = 792.
Then, using the same program, I calculate external capacitance ( formula f = 1/[2π*(LC)^(1/2)] is used ):
external capacitance = 76.758 pF.
Moreover, the program calculates characteristic resistance of the LC circuit:
characteristic resistance ρ = 20.735 Ohm.
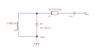
I don't understand, what is characteristic resistance and how can I depict this quantity in scheme of the RF coil. I assumed that characteristic resistance can be represented as a resistor with R1 = 20.735 Ohm. Is it right? Please find attached the scheme of the RF coil.

It is known that RF coils should be connected to MRI system using coaxial cable with impedance Z = 50 Ohm. From the scheme, one can see that there are two capacitors - tuning and matching. Tuning capacitor Ct is connected to the inductor in parallel, and matching capacitor Cm is placed between R1 and power source P1. How can I calculate capacitance of the matching capacitor Cm?
Can I use 50 Ohm coaxial cable of arbitrary length or should I calculate the length of the coaxial cable too?

 

[zoki85]

Characteristic "resistance" or better say characteristic impedance is simply the ratio Z_c=√(L/C) in lumped LC circuits or the ratio √(L'/C') in distributed LC circuits. This figure directly has got nothing to do with loses in the circuit. Indirectly it has because when divided by R it determines the Q factor of the circuit (and higher that factor smaller are the relative loses in the circuit). BTW, output of the program Q=792 for your example is way off the chart: in real world Q will be much lower than that (probably <100). Matching capacitance you calculate that input impedance of the network be as closer as possible to the source impedance. When Z_in=Z_s there is no reflection of electromagnetic energy and length of the coax is not a thing to worry about.

 

[tech99]

I am wondering if "p" is actually intended to be loss resistance.
By the way, 20mm is a very small coil and I think the losses may be high. If possible I think 2 turns would give better Q.
In the matching circuit shown, if R1 is the coil resistance, it is shown in the wrong place.

 

[Leonid92]

Characteristic "resistance" or better say characteristic impedance is simply the ratio Z_c=√(L/C) in lumped LC circuits or the ratio √(L'/C') in distributed LC circuits. This figure directly has got nothing to do with loses in the circuit. Indirectly it has because when divided by R it determines the Q factor of the circuit (and higher that factor smaller are the relative loses in the circuit). BTW, output of the program Q=792 for your example is way off the chart: in real world Q will be much lower than that (probably <100). Matching capacitance you calculate that input impedance of the network be as closer as possible to the source impedance. When Z_in=Z_s there is no reflection of electromagnetic energy and length of the coax is not a thing to worry about.

Thanks a lot!
I've just checked ρ value - it is approximately 20.735 Ohm ( √(L/C) ) as program Coil32 says.
As I remember, Q = ωL/R. Q value obtained in the program is 792, ω = 2πf = 2π*10^8 (rad/s), L = 0.033*10^(-6) H. Thus: R = ωL/Q = 0.026 Ohm.
On the other hand, R = ρ1*length/S, where ρ1 designates specific electrical resistance of copper (0.017 [Ohm*mm^2]/m), length is a length of copper conductor (length = πD, where D is a diameter of the loop, D = 0.02 m), and S is a cross-sectional area of the copper wire (S = [πd^2]/4, where d is a wire diameter, d = 2 mm). Thus: R = 0.00034 Ohm.
Could you please explain this discrepancy: R = 0.026 Ohm vs R = 0.00034 Ohm?

 

[Leonid92]

I am wondering if "p" is actually intended to be loss resistance.
By the way, 20mm is a very small coil and I think the losses may be high. If possible I think 2 turns would give better Q.
In the matching circuit shown, if R1 is the coil resistance, it is shown in the wrong place.

Thank you for your answer!
ρ (Greek "rho") is characteristic resistance, or more correctly - characteristic impedance as zoki85 wrote.
By placing resistor R1 in the scheme I tried to introduce characteristic resistance of LC circuit - it was a mistake. Because characteristic resistance (impedance) is determined only by L and C - I forgot this fact, although I've read an electrical engineering textbook recently.

 

[Leonid92]

Link to the Coil32 program: https://coil32.net/
Link to the formulas for calculation of inductance of one turn loop coil: https://coil32.net/one-turn-loop-coil.html

 

[zoki85]

Thanks a lot!
I've just checked ρ value - it is approximately 20.735 Ohm ( √(L/C) ) as program Coil32 says.
As I remember, Q = ωL/R. Q value obtained in the program is 792, ω = 2πf = 2π*10^8 (rad/s), L = 0.033*10^(-6) H. Thus: R = ωL/Q = 0.026 Ohm.
On the other hand, R = ρ1*length/S, where ρ1 designates specific electrical resistance of copper (0.017 [Ohm*mm^2]/m), length is a length of copper conductor (length = πD, where D is a diameter of the loop, D = 0.02 m), and S is a cross-sectional area of the copper wire (S = [πd^2]/4, where d is a wire diameter, d = 2 mm). Thus: R = 0.00034 Ohm.
Could you please explain this discrepancy: R = 0.026 Ohm vs R = 0.00034 Ohm?

I didn't calculate a single thing here, but I guess the program somehow calculates increased resistance due to "skin effect" at 100 Mhz. However it doesn't care about capacitor loses, proximity loses, contact loses, EM radiation etc. Therefore in real world Q factor will be several times lower than given by the program

 

[Baluncore]

The frequency is specified as 100 MHz, the diameter as 20 mm, the characteristic impedance of the connection cable as 50R.
One additional parameter is required before the design of the neutralised inductor and coupling network can be completed. That is the overall bandwidth, the rise-time or the Q of the network.

The frequency dependent skin effect will change both the Q and the inductance of a coil.

An optimum design may require an inductor with more than one turn. If only one turn is used then an RF transformer or resistive network may be required.

 

[Leonid92]

The frequency is specified as 100 MHz, the diameter as 20 mm, the characteristic impedance of the connection cable as 50R.
One additional parameter is required before the design of the neutralised inductor and coupling network can be completed. That is the overall bandwidth, the rise-time or the Q of the network.

The frequency dependent skin effect will change both the Q and the inductance of a coil.

An optimum design may require an inductor with more than one turn. If only one turn is used then an RF transformer or resistive network may be required.

Thank you for your answer!
Could you please recommend a book where I can find the information about all parameters mentioned in your post and design of the neutralised inductor and coupling network in more detail?

 

[Baluncore]

The bandwidth, rise-time or the Q of a network are all the same thing, just expressed in different ways.

Maybe start with;
Radio Engineers' Handbook. Terman. 1943. Section 3. Circuit theory.
https://www.qsl.net/va3iul/Files/Old_Radio_Frequency_Books.htm

 

[Leonid92]

The bandwidth, rise-time or the Q of a network are all the same thing, just expressed in different ways.

Maybe start with;
Radio Engineers' Handbook. Terman. 1943. Section 3. Circuit theory.
https://www.qsl.net/va3iul/Files/Old_Radio_Frequency_Books.htm

Thank you!
After studying circuit theory, is it necessary to study antenna theory in order to develop RF coils for MRI?

 

[Baluncore]

No. The pickup inductor is a small loop antenna. You must match it to the 50 ohm line with minimum signal attenuation. It must be matched over the required frequency band.