Basis of a Tensor Product - Theorem 10.2 - Another Question

[Math Amateur]

I am reading Bruce N. Coopersteins book: Advanced Linear Algebra (Second Edition) ... ...

I am focused on Section 10.1 Introduction to Tensor Products ... ...

I need help with another aspect of the proof of Theorem 10.2 regarding the basis of a tensor product ... ...Theorem 10.2 reads as follows:

A diagram involving the mappings $\iota$ and $\gamma'$ is as follows:

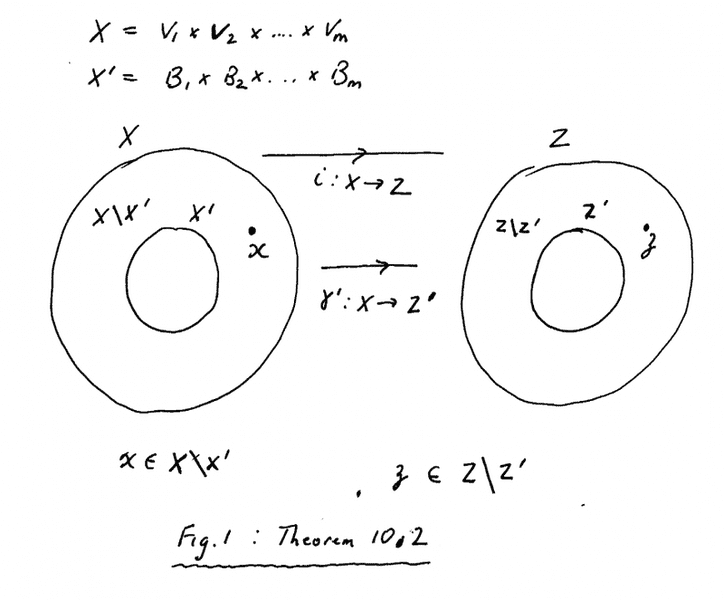
My questions are as follows:Question 1

How do we know that there exists a multilinear map $\gamma' \ : \ X \longrightarrow Z'$ ?
Question 2What happens (what are the 'mechanics') under the mapping $\gamma'$ ... ... to the elements in X\X' ( that is $X - X'$)? How can we be sure that these elements end up in $Z'$ and not in Z\Z'? (see Figure 1 above)
Hope someone can help ...

Peter

 

[andrewkirk]

Re question 1:
Let $V^\dagger\equiv V_1\times,...,\times V_m$ and let's use angle brackets $\langle...\rangle$ to enclose components of Cartesian product spaces. Let the components of $\mathscr{B}_j$ be $v_{j1},...,v_{jn_j}$ where $n_j$ is the dim of $V_j$.
You haven't said what $Z$ is but let's assume it's the infinite-dimensional vector space over field $F$ with base set
$$\mathscr{B}^Z\equiv \{\langle u_1,...,u_m\rangle\ |\ \forall k:\ u_k\in V_k\}$$
More formally, $Z$ is the set of all functions from $\mathscr{B}^Z$ to $F$ for which each such function has finite support (ie is nonzero on only finitely many input values).
$Z'$ is the subset of $Z$ containing only functions whose support lies in $X'$, and it is easily shown to be a subspace.
Define the map $\xi:X'\to Z'$ that maps each Cartesian product of basis vectors $\langle v_{1i_1},...,v_{mi_m}\rangle$ to the function that returns zero for every input except $\langle v_{1i_1},...,v_{mi_m}\rangle$, for which it returns $1_F$. Note that the image of $\xi$ is a basis for $Z'$.
Then a map $\gamma':V^\dagger\to Z'$ is multilinear, and agrees with $\xi$ on $X'$, if and only if it satisfies:
\begin{align*}
\gamma'\left(\left\langle \sum_{i_1}a_{1i_1}v_{1i_1},\, ...\, ,\sum_{i_m}a_{mi_m}v_{mi_m}\right\rangle\right)
&=\sum_{i_1}\sum_{i_2}\ ...\ \sum_{i_m} \prod_{k=1}^m a_{ki_k}\gamma'\left(\left\langle
v_{1i_1},\, ...\, ,v_{mi_m}\right\rangle\right)
\\&=
\sum_{i_1}\sum_{i_2}\ ...\ \sum_{i_m} \prod_{k=1}^m a_{ki_k}
\xi\left(\langle v_{1i_1},...,v_{mi_m}\rangle\right)
\end{align*}
where the first equality implements multilinearity and the second implements the requirement to agree with $\xi$.
Since $X'$ is a basis for $V^\dagger$, it follows that such a map $\gamma'$ exists. It is unique because the representation $\sum_{i_k}a_{ki_k}v_{ki_k}$ of the $k$th coordinate of the input to $\gamma'$ is unique.

 

[Math Amateur]

Andrew,

Going through your post carefully shortly ...

Cooperstein provides a definition of Z in the introduction to Section 10.1 including in the proof of Theorem 10.1 ...

Relevant text from Cooperstein is as follows:

Hope that helps ...

Peter