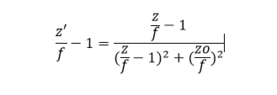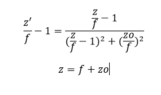Beam Expansion: Distance between 2 lenses in a Keplerian beam expander

tanhanhbi
Messages
9
Reaction score
3
Homework Statement
Determine the optical distance d between the lenses such that the distance z′ to the waist of the final beam is as large as possible.
Relevant Equations
Gaussian beam
1694753568777.png

Basically this is the Exercise In Fundamentals of Photonics book.
We also need to use these two equation (1) and (2)
1694757157317.png

As we all know, in order to make the z' as far as possible, we must place 2 lens with this distance
1694754359557.png

I already figure that thank to the initial condition of the first lens position
1694754562581.png

So that the z1 must equal to f1
1694754616697.png

For the z2, I tried to replace zo in (2) onto (1), then take the derivative of z' with respect to z2. My initial though that let the derivative of z' equal to 0, we can find the maximal of z'. But actually after finish the derivative thing, z' do not have maximal and I already always infinity ?
1694757110830.png

So I am not sure what wrong with my thinking. If someone could give me a clue, I really appreciate it.
 

Attachments

  • 1694754075958.png
    1694754075958.png
    3.2 KB · Views: 97
  • 1694754132747.png
    1694754132747.png
    3.9 KB · Views: 104

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

TM modes between 2 parallel plates with 2 dielectrics
Replies
6
Views
1K
Numerical aperture of a Keplerian telescope
Replies
1
Views
3K
Closest distance of approach between 2 charged particles
Replies
5
Views
1K
A Post-Selection: Pre-existing Correlations or Action At A Distance?
2
Replies
54
Views
6K
Possibly solved the metric without field equations
Replies
11
Views
2K
MATLAB Communication between Arduino and Matlab Help
Replies
1
Views
3K
Electric potential energy between charge and moving magnet
Replies
7
Views
2K
Logic of GR as mathematically derived
Replies
41
Views
8K
Questions on Redshift, Hubble’s Law, spacetime expansion and the standard model
Replies
21
Views
4K
Challenge Math Challenge - November 2018
4
Replies
175
Views
25K

Hot Threads

Recent Insights

Back
Top