Behavior of charged particles in a speed selector

[greg_rack]

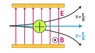
Considering the device above, which uses electric and magnetic fields placed properly to avoid charged moving particles with velocities different from the ratio $\frac{E}{B}$ to exit, getting deflected upwards or downwards. All that is easily demonstrable by equalling the forces acting on the particle: $qE=qvB$.
Now, my question is: what happens to particles with $v\neq \frac{E}{B}$?
What I found online if $v>\frac{E}{B}$ Lorentz's force will be greater(since it's proportional to speed) than the electric one, so the particle will get deflected upwards; otherwise, if $v<\frac{E}{B}$, the electric force will "win" so the particle will move downwards... but this explanation doesn't satisfy me:
what if the electric field is much greater than the magnetic one, and even if $v>\frac{E}{B}$, $E>vB$ and vice-versa?
Shouldn't we know the magnitude of both fields to predict the behavior of particles with $v\neq \frac{E}{B}$?

 

[Vanadium 50]

If v > E/B, then E is less than vB. It cannot then be greater than vB.

 

[anuttarasammyak]

Hello.
Lorentz force including electric field makes the charged particle move as
$$\mathbf{F}=q(\mathbf{E}+\mathbf{v} \times \mathbf{B})=\frac{d \mathbf{p}}{dt}$$
we should solve this equation of motion to know its motion. By solving the equation we know its velocity is cyclic in time with drifting speed of $\frac{E}{B}$ in time average. The trajectories are trochoids.

So your first v=E/B case is the special setting that this time average speed is an actual speed and the trajectory is a line.

 

[greg_rack]

If v > E/B, then E is less than vB. It cannot then be greater than vB.

Right, that's what I was missing... thanks for the hint!