Bell's Spaceships Paradox explained.

[Fredrik]

It is important to think back to instance 2 where we agreed that there is no relativistic difference between the space station tossing a rock and the two rockets tossing rocks simultaneously in their starting frame. From here say that the simultaneity of the rockets is still in tacked because if we looked at if from the spaceship tossing a rock then it is quite clear that the rockets are completely unaffected in their still stationary frame.

OK, I get what you're saying. You're not making a mistake here. The mistake was in instance 2. I was wrong to agree with it.

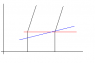
If the space station tosses a rock, that can't be equivalent with the rockets tossing one rock each. I have uploaded another ugly space-time diagram to show why.

The diagram shows the world lines of both rockets, in a coordinate system where they are initially at rest, as they give themselves a boost by tossing a rock each. This happens where the world lines intersect the red line. Events on the red line are simultaneous in this frame. Events on the blue line are simultaneous in any frame that's co-moving with one of the rockets at any event on that rocket's world line after that rocket tosses its first rock and before it tosses its second rock. In particular, events on the blue line are simultaneous in the frame that's co-moving with rocket B (the world line on the right) immediately after its first toss. So in rocket B's frame, right after its first toss, rocket A hasn't tossed its first rock yet.

This proves that the situations are not equivalent.

(I hope it's not confusing that I accidentally swapped the meaning of red and blue from my last diagram).

I believe you use the earlier definition for simultaneous in instance 1-2, but use the latter in instance 3. And this change in convention is causing the confusion.

That is absolutely not true. I'm always using the standard definition of simultaneity.

What I call simultaneous takes the travel time of light into account, ei something I see 1 light second away happened 1 second ago, it is not happening right now. The other way is to say what you see now is what is happening now.

That definition of simultaneity would be very confusing and probably also useless. Open any book on SR and you will see that that's not how they do it. This is how they do it:

Assume that both space and time have the same properties at every event, and that the speed of light is c in every inertial frame. Now pick one of those inertial frames and suppose that there's a mirror at some point along the x axis. Suppose also that you emit light from x=0, in the positive x direction, at t=-T, and that it's reflected by the mirror and returns to x=0 at t=T. Now the reflection event must have been simultaneous with the event t=0,x=0. That implies that we must assign time coordinate 0 to the reflection event, and the fact that the speed of light is c implies that we must assign the x coordinate cT to the reflection event.

You could, alternatively, start with the definition of Minkowski space and use that to define the inertial frames mathematically.

Either way, this simple statement will always hold: Two events are simultaneous in an inertial frame if they have the same time coordinate in that frame.

 

[MeJennifer]

something I see 1 light second away happened 1 second ago, it is not happening right now.

What you see is nothing but photons hitting your retina, it is not something away, it is a local event.

 

[peter0302]

So the bottom line is when two objects are separated in space and begin acclerating at the same time with the same proper acceleration, their clocks will not stay in sync. So if they both instantaneously accelerate to .5c, the front rocket will believe the rear rocket hasn't even started moving yet, and the rear rocket will think the front rocket had a huge head start.

Is that right?? That's the only way the Bell argument can work.

 

[yuiop]

I guess the thing that bothers me about this is the whole simulatanity idea and what exactly it mean when. The way I see it is that anytime you view an object with a velocity (I'm leaving gravity out of this for simplicity) you lose simualtanity. I.e. you get the ladder through the barn. But when I think about this I look at it as instances. For example:
Instant 1) Everything is at rest (no contraction, velocities, and everything is simulataious.
Instant 2) The 2 rockets toss out a rock (for simplicity I like rocks because its instantanious change in velocity) and have the a change in velocity. At this time the spacestation no longer shares a common frame and it losses simualtanialty w/r/t the rockets. (I do not see how this is any differnt than if the space station tossed a rock in the other direction and left the 2 rockets in place.)
Instant 3) The station now views the back rocket tossing the rock before the front rocket does. This tells me that it would appear as though the back rocket is accelerating faster and catching up to the back rocket. (all the while both rockets are still seeing each other sitting still, again just as the spacestation was launching rocks.)
Instant 4) Instant 3 would continue until from the spacestations view the back rockets stops tossing rocks and then the front rocket would finish tossing rockets leaving the distance between the 2 rockets shortented (contacted) and constant because they would both now have the same velocity according to the space station. (From the view of the rockets they have never moved in relation to each other.

Insite as to this flaw would be wonderful. =)

...
Instance 2 - I believe most people accept this. To disprove this one would have to show that there is a relativistic difference between the station tossing a rock and the rockets simualtanialty tossing rocks, ie the view from one frame to another is not identical in length contraction, time dilation etc. There are of course non relativistic differences, who tossed rocks, mass changes etc.

...The mistake was in instance 2. I was wrong to agree with it...

Hi Wizardblade,
Fredrik was right to disagree (eventually) with instance 2 and everything that follows from that conclusion. There IS a relativistic difference between the station tossing a rock and the rockets simultaneousy tossing rocks. When the space station toses rocks he sees the the rockets getting progressively closer together while the the rockets see themselves as remaining a constant distance apart. That is NOT equivalent to the situation described in the classic Bell's rockets paradox. When the rockets toss rocks simultaneously according to the space station they ramain a constant distance apart as measured by the spacestation, while the rocket observers will measure there separation distance to be increasing over time.

 

[yuiop]

By the way, your description of what should happen in Bell's spaceship scenario (rocks being thrown at the same time in co-moving frames) is a description of Born rigid acceleration of two points that are infinitesimally close. (I'm actually not 100% sure that they need to be infinitesimally close. I should probably give that some thought).

As far as I can recall, observers at the tail and nose of a rocket undergoing perfect and constant Born rigid acceleration will measure their separation distance to remain constant over time no matter how long the rocket is.

This wikipedia article on Rindler Coordinates supports my assertion above. http://en.wikipedia.org/wiki/Rindler_space#Notions_of_distance

"There are other notions of distance, but the main point is clear: while the values of these various notions will in general disagree for a given pair of Rindler observers, they all agree that every pair of Rindler observers maintains constant distance. The fact that very nearby Rindler observers are mutually stationary follows from the fact, noted above, that the expansion tensor of the Rindler congruence vanishes identically. However, we have shown here that in various senses, this rigidity property holds at larger scales. "

The "rigidity property" they talk of here is the property of the mutual separation of rindler observers remaining constant over time and not the usual meaning of a rigid body being infinitely incompressable.

 

[yuiop]

So the bottom line is when two objects are separated in space and begin acclerating at the same time with the same proper acceleration, their clocks will not stay in sync. So if they both instantaneously accelerate to .5c, the front rocket will believe the rear rocket hasn't even started moving yet, and the rear rocket will think the front rocket had a huge head start.

Is that right?? That's the only way the Bell argument can work.

That is the way I visualise the situation.

 

[peter0302]

Ok so now another question - if that's right - WHEN does the string break? It clearly cannot break right away - because then it would be breaking in the PAST of the S frame.

 

[Wizardsblade]

Can't we test this? Isn't this equivalent to a charged particle (the space station) and a wire without current (the electrons are the rockets and at rest). When we apply current we give the “rockets” velocity and we can do the math to see if they contract or stay the same distance apart in the “space stations” frame.

 

[Fredrik]

So the bottom line is when two objects are separated in space and begin acclerating at the same time with the same proper acceleration, their clocks will not stay in sync.

Yes, that's right. The clocks show the same times at events that are simultaneous in the original rest frame, but they don't show the same time at events that are simultaneous in a frame that's co-moving with one of the rockets.

So if they both instantaneously accelerate to .5c, the front rocket will believe the rear rocket hasn't even started moving yet, and the rear rocket will think the front rocket had a huge head start.

Is that right?? That's the only way the Bell argument can work.

Yes, that's exactly how it works.

Ok so now another question - if that's right - WHEN does the string break? It clearly cannot break right away - because then it would be breaking in the PAST of the S frame.

It does break right away. Let's say that it breaks by disconnecting itself from rocket B. This event is located where the blue line intersects the world line of rocket B (the one on the right in the diagram). This event has a higher time coordinate (in the original rest frame) than the event where rocket B tossed its first rock, so it doesn't occur in the past.

Both rockets agree that the string broke because rocket B took off first.

It's not a problem that this event is simultaneous in B's frame with events that are in the past in S's frame. What matters is that there is no inconsistency when you describe all events from one frame. All the "paradoxes" of SR are the result of incorrectly describing different parts of the story in different frames.

 

[Hurkyl]

What I call simultaneous takes the travel time of light into account, ei something I see 1 light second away happened 1 second ago, it is not happening right now.

How do you measure that distance, without first having a notion of simultaneity?

 

[Wizardsblade]

something I see 1 light second away happened 1 second ago, it is not happening right now.

Assume that both space and time have the same properties at every event, and that the speed of light is c in every inertial frame. Now pick one of those inertial frames and suppose that there's a mirror at some point along the x axis. Suppose also that you emit light from x=0, in the positive x direction, at t=-T, and that it's reflected by the mirror and returns to x=0 at t=T. Now the reflection event must have been simultaneous with the event t=0,x=0. That implies that we must assign time coordinate 0 to the reflection event, and the fact that the speed of light is c implies that we must assign the x coordinate cT to the reflection event.

What you see is nothing but photons hitting your retina, it is not something away, it is a local event.

How do you measure that distance, without first having a notion of simultaneity?

Do you guys not see that what I said is equivalent to what Fredrik said? Make T=1 second so that -T = -1 second then it is clear that at x = 1 light second t=0 simultaneously with x=0, t=0. Ergo what I am currently seeing with my eyes at a distance x=1 light second is what happened when my T=-1 second. I just do not have the finesse that Fredrik has =).

 

[Fredrik]

OK, I'm glad we agree. I misunderstood you then.

 

[MeJennifer]

Ergo what I am currently seeing with my eyes at a distance x=1 light second is what happened when my T=-1 second. I just do not have the finesse that Fredrik has =).

We cannot see at distances, that is just popular speak.

What you are currently seeing with your eyes are photons hitting your retina with a distance of 0 and it is happening now. Yes these photons have an origin but so does a tennis ball hitting one's head. Would you say that you feel a tennis ball currently hitting your head from a distance that happened in the past?

 

[peter0302]

Ok, now that's nitpicky.

 

[Wizardsblade]

We cannot see at distances, that is just popular speak.

What you are currently seeing with your eyes are photons hitting your retina with a distance of 0 and it is happening now. Yes these photons have an origin but so does a tennis ball hitting one's head. Would you say that you feel a tennis ball currently hitting your head from a distance that happened in the past?

This is off topic, but our eyes (plural) can distinguish distance by triangulation. Of course we only see what is currently hitting our eyes, hence the definition of simultaneity is not what we see but rather what has already been stated above.