B General Questions about Special Relativity

[Herman Trivilino]

How about the speed of light being constant, though? Isn't that something we only know from experiment and not something we deduced from other facts which were already known?

It follows as a consequence of Maxwell's theory of electromagnetism, but experimental verification is needed to know that that is indeed the right way to interpret those laws of electromagnetism.

Nature behaves the way it behaves. Physical laws are generalizations from observations of those behaviors. As humans we like to pretend that Nature obeys the laws of physics, but that's an anthropomorphism.

 

[NoahsArk]

Physical laws are generalizations from observations of those behaviors. As humans we like to pretend that Nature obeys the laws of physics, but that's an anthropomorphism.

Doesn't nature obey it though? Aren't the equations of physics not subject to change? If a certain object of a certain weight is dropped from a certain height, we can calculate exactly when it will hit the ground, and that should never change if all the conditions are the same.

Also, on the idea of the constancy of the speed of light, here is an example which I read to explain it: If a rocket is traveling at .75C with respect to me, and that rocket shines a beam of light, I would expect that someone in the rocket would measure the beam at .25C. However, if I know that his measuring sticks are four times smaller than mine, it will come as no surprise that his measurement of C will be equal to mine. For example, if the rocket were traveling at .75C and chasing a beam of light that traveled a distance of one light year, and the rocket traveled .75 light years, I would see the beam being .25 light years ahead of him. With his meter stick, though, he'd measure that .25 distance to be 1. That would make sense if it weren't for the fact that the lengths he is measuring also contracted, which would cancel out the effects of his meter stick being contracted. How to make sense of this?

 

[Orodruin]

Doesn't nature obey it though? Aren't the equations of physics not subject to change? If a certain object of a certain weight is dropped from a certain height, we can calculate exactly when it will hit the ground, and that should never change if all the conditions are the same.

But this is just an assumption on the repeatability of experiments. It is an assumption that has served us well and is well tested experimentally. Ideally though, a physical theory should make new predictions that you can test. If it does not match the new tests, we should be looking to replace it with something more accurate - as was done when Newtonian mechanics was surpassed by relativistic mechanics. It does not mean that Newtonian mechanics is wrong - within its limited region of applicability - but special relativity is more accurate. You have to differentiate how nature behaves with our description of how nature behaves, it is the latter we are all too fond of calling "laws of nature".

How to make sense of this?

You are not taking relative simultaneity into account. There is more to this than length contraction and you need to combine all relativistic effects, including the relativity of simultaneity, into account in order to make sense of it. I suggest any elementary textbook on relativity.

 

[Herman Trivilino]

Doesn't nature obey it though?

No. Nature behaves the way it behaves. It makes no anthropomorphic effort to obey anything.

Aren't the equations of physics not subject to change?

The laws of physics are indeed subject to change.

If a certain object of a certain weight is dropped from a certain height, we can calculate exactly when it will hit the ground, and that should never change if all the conditions are the same.

No. We cannot calculate anything exactly. The best we can ever do is an approximate measurement. All measurements are subject to uncertaintly based on the devices we use to make the measurements. There's no such thing as an exact measurement.

With his meter stick, though, he'd measure that .25 distance to be 1.

No, he wouldn't. He would measure it to be smaller, not four times larger.

 

[Nugatory]

How to make sense of this?

In post #3 of this thread, all the way back on the first page, I said "Back away from trying to intuitively understand length contraction and time dilation, work on nailing down your understanding of relativity of simultaneity." This new problem isn't making sense to you because you're forgetting the relativity of simultaneity again.

We could put a bomb triggered by the light flash at the 1.0 point (using your measurements), and another bomb triggered by collision with the ship at the .75 point (again, using your measurements). You will find that both bombs explode AT THE SAME TIME, meaning that the ship was at the .75 point AT THE SAME TIME that the light was at the 1.0 point. 1.0-.75=.25 so clearly the light was .25 light years ahead of the ship. However, the two explosions are not simultaneous in the ship frame, so the ship's measurement of the distance between them tells you nothing about how far ahead the light was in the ship frame - to do that measurement you'd need to find where the light was and where the ship was AT THE SAME TIME in the ship frame, measure the distance between those points.

 

[NoahsArk]

I suggest any elementary textbook on relativity

Thanks. I got the Wheeler book- Space Time Physics. Hopefully it will be covered there. It starts out with the space time interval ehich I think is an interesting place to start, because in the examples it seems like he assumes people already know that two observers in different frams can measure time differently.

Regarding the point about the way nature behaves vs our descriptions of it, does that mean we have laws, but they are refined and become more general as we get more info (e.g Galilean relativity vs. special relativity). Also, couldn't it be that there are laws that can't be refined or generalized further?

Nugatory, the example you used involves teo events in teo different places. I need to think more about how relativity of simultaneity relates to the measurement of objects. E.g. On the rocket the clocks in a different rows are out of synch w each other in the frame stationary w. Respect to the rocket. That relates to clocks though... Would this apply to just the distance between two points on the rocket when no events are involved?

 

[Nugatory]

Regarding the point about the way nature behaves vs our descriptions of it, does that mean we have laws, but they are refined and become more general as we get more info (e.g Galilean relativity vs. special relativity). Also, couldn't it be that there are laws that can't be refined or generalized further?

You might want to give this essay a try: http://chem.tufts.edu/AnswersInScience/RelativityofWrong.htm
(Start a new thread for any followup on this fork of the discussion, please)

 

[Nugatory]

Would this apply to just the distance between two points on the rocket when no events are involved?

An "event" is just a point in space at a particular time, so all measurements always involve events. If you say "here" and tap your finger on a point in space, you've just identified an event: the point where your fingertip was at the moment of the tap. If I say "one meter to my left, level with my navel, six meters straight in front, three minutes from now" that's an event even if nothing noteworthy happens at that spot three minutes from now.

All distance measurements involve two events: "the point where one end of the length being measured was at a given time" and "the point where the other end of the length being measured was at the same time".

 

[Herman Trivilino]

Regarding the point about the way nature behaves vs our descriptions of it, does that mean we have laws, but they are refined and become more general as we get more info (e.g Galilean relativity vs. special relativity). Also, couldn't it be that there are laws that can't be refined or generalized further?

If you just google richard feynman layers of an onion you'll find lots of references to this question. It may be that as scientific knowledge of one particular thing or another progresses we will keep refining our knowledge. Like peeling an onion to always find another layer below. Or it may be that as we peel it we eventually reach a core, something that can no longer be refined and is universally valid. The only way to find out is to keep looking. Nature will turn out to be the way it turns out to be. You can't know unless you investigate.

 

[Ebeb]

...
Also, on the idea of the constancy of the speed of light, here is an example which I read to explain it: If a rocket is traveling at .75C with respect to me, and that rocket shines a beam of light, I would expect that someone in the rocket would measure the beam at .25C. However, if I know that his measuring sticks are four times smaller than mine, it will come as no surprise that his measurement of C will be equal to mine. For example, if the rocket were traveling at .75C and chasing a beam of light that traveled a distance of one light year, and the rocket traveled .75 light years, I would see the beam being .25 light years ahead of him. With his meter stick, though, he'd measure that .25 distance to be 1. That would make sense if it weren't for the fact that the lengths he is measuring also contracted, which would cancel out the effects of his meter stick being contracted. How to make sense of this?

No, for the astronaut at that event, per his frame the light is not at distance 1 from him. It's at .66 ! In this post I explain you how it works.
Furthermore, your 'that distance' is a measurement between two events that are simultaneous for me, but not simultaneous for the rocket astronaut.
And the astronaut does not measure with a contracted tape measurer. Only for me, per my frames of simultaneous events, his measuring stick is contracted (due to different events of the measuring stick being simuiltaneous for him or me). For the astronaut, his wristwatch does not run slow and his measuring stick does not contract. What does happen is that for him my clock runs slow, and my measuring stick is contracted, but that's irrelevant for the measurements he performs.

Consider following 3 events:
Event 1: astronaut at his location after .75 lightyears: Let's say he is at star A
Event 2: light at star B (star B located further than star A)
Event 3: light at star C (star C located further than star B)

v = .75c
gamma = 1.5

1/ I stayed home on earth.
For me the distance from Earth to star A is .75 ly.
For me the distance from Earth to star B is 1 ly.
For me the distance between star A and B is .25 ly.
For me the distance from Earth to star C is 1.75 ly.
For me, events 1 and 2 are simultaneous. 1 and 3 are not.
For me, when my wristwatch shows 1, the rocket is at star A and the light is at star B.
For me, when the rocket traveled .75 ly, the light traveled 1 ly.
For me and for the astronaut, when the rocket is at star A, the astronaut's wristwatch shows .66 (content of event is absolute)!

2/ The astronaut frame:
For the rocket astronaut events 1 and 3 are simultaneous.
For him, when the rocket is at star A -and his wristwatch shows .66, the light is (already) at star C.
(Due to relativity of simultaneity of events, per my frame the light will be at star C when the rocket is somewhere between star B and C)
Per astronaut frame, the distance he traveled to star A is .5 ly (=.75/1.5). His clock indicates .66 (1/1.5), speed = .75c
For the astronaut the distance between star A and B is .166 lightyears. Between star B and C the distance is .5. From A to C = .66

At event 1, when the astronaut is at star A -and his wristwatch indicates .66- , per astronaut frame the light has traveled .66 ly from astronaut to star C. Hence per astronaut frame light speed is c, because .66/.66=1

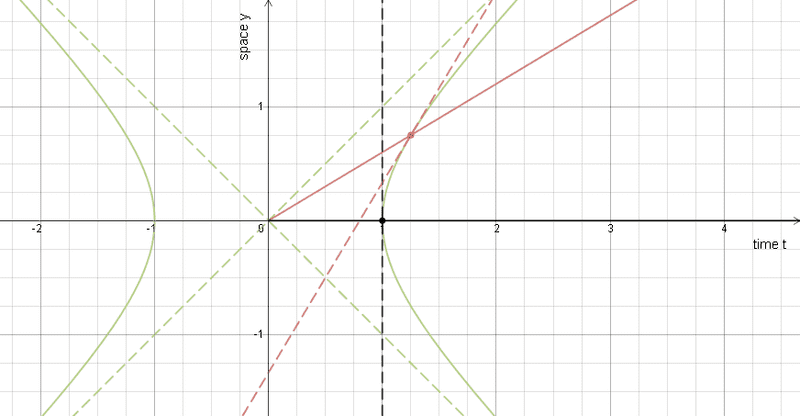
You can find all this information in my spacetime diagram below:

 

[soy252]

I just need some clarification but if one person goes . 5c relative to Earth in one direction and another person goes .5 c in the other direction then wouldn't each person be going to speed of light relative to the other person? I'm sure that there is some sort of flaw in this thought experiment but could someone explain this to me?

 

[Ibix]

I just need some clarification but if one person goes . 5c relative to Earth in one direction and another person goes .5 c in the other direction then wouldn't each person be going to speed of light relative to the other person? I'm sure that there is some sort of flaw in this thought experiment but could someone explain this to me?

Velocities do not add that way. The immediate cause of that is that a moving object's rulers are length contracted, their clocks are time-dilated, and also de-synchronised due to the relativity of simultaneity. So its notions of time and distance and, hence, velocity do not match up with your intuition. If there are two objects with velocities u and v in a given frame then according to the first one the second has velocity $$v'=\frac {v-u}{1-uv/c^2} $$In your case, with velocities of ±0.5c, you get 1/1.25=0.8c. Note that for everyday velocities, $1-uv/c^2\simeq 1$, and the formula reduces to what you expect.

 

[Herman Trivilino]

I just need some clarification but if one person goes . 5c relative to Earth in one direction and another person goes .5 c in the other direction [...]

Earth would indeed see the distance between those two people increase at the speed of light.

Each of them would, on the other hand, see Earth moving at a speed of $0.5c$.

But, each of them would see the other moving at a speed of $0.8c$.

 

[pr3dator]

It is true. The tailllings question you can tell why nature works this way?
I try.
When you draw it in spacetime diagram you will see how it is works.
Whatever your speed is , the "lightspeed" related to you will be on lightcone always.
The two moving observers with +-0.5c have same lightcone. (pinned into common/starting point of spacetime)
Now we see that it is impossible the c value of difference between.

 

[Ebeb]

Adding velocities on spacetime diagram.

Let's consider 3rd observer: black reference system.
Relative to black reference frame the orange observer travels .4513c per 1 time unit
Relative to black reference frame the green observer travels -.4513c per 1 time unit

Adding velocities (Newton way) would mean relative velocity between orange and green frame = 0.4513c + 0.4513c = .9c
However, by using the relativistic equation for adding velocities
U = (v-(-u))/((1- (-vu))/c2) = .9026/1.2036 = 0.75c

On diagram same scale for green and orange x and t units (because symmetrical to orthogonal black axes).
Different scale for black units (smaller than green and orange x and t units).

(PS. v and gamma top right of dwg is for green relative to orange (and orange relative to green))

 

[robphy]

Let me suggest this tick-supplemented Minkowski spacetime diagram for velocity-addition.
[It's taken from my article described in my Insight although it's not in the Insight itself.]
(I think Loedel-type diagrams okay, but are of limited value.)

I think you can clearly see that the relativity of simultaneity is an important feature of velocity-addition.

 

[NoahsArk]

Thank you very much Ebeb and robphy for the diagrams, and to everyone who's helped me with this.

I plan to study the diagrams further, and to also work out more the example that you gave Ebeb.

Earlier I was wondering why, in a space time diagram, both the time and space axis are tilted inwards for the moving frame compared to the stationary frame's set of axis. Now, after looking at the diagrams, I see the reason I think: the angle between the beam of light and the space axis has to be equal to the angle between the beam of light and the time axis. In the stationary frame, the angle is 45% from both the space and time axis. For someone traveling at half the speed of light, the angle has to be 22.5% from each axis (which is similar to the orange reference frame). If only the space axis were tilted but not the time axis, it would mean that the beam was going faster than light I think.

 

[Orodruin]

If only the space axis were tilted but not the time axis, it would mean that the beam was going faster than light I think.

Note that in Galilean relativity only the time axis is tilted. The space axis being tilted is what is new in SR.

 

[robphy]

Careful... For a slope of 0.5 (with respect to the t-axis), the angle in degrees is
arctan(.5) = 26.5650512 degrees
(Google "arctan(.5) in degrees". Similarly, you can compute
tan(22.5 degrees)=0.41421356237.)

 

[robphy]

The geometric reason for the tilting of the "space axes" is due that axis being tangent to the "circle" ( a hyperbola in special relativity ).

Consult this post from a past thread...
https://www.physicsforums.com/threads/minkowski-diagram.876359/#post-5503686
Play with the interactive desmos visualization.

 

[Orodruin]

The geometric reason for the tilting of the "space axes" is due that axis being tangent to the "circle" ( a hyperbola in special relativity ).

You mean normal, i.e., with a tangent vector orthogonal to the tangent vector of the hyperbola at the point they cross. This is just like a rotation in Euclidean space, the axes cross a circle at right angles.

 

[robphy]

The geometric reason for the tilting of the "space axes" is due that axis being tangent to the "circle" ( a hyperbola in special relativity ).

You mean normal, i.e., with a tangent vector orthogonal to the tangent vector of the hyperbola at the point they cross. This is just like a rotation in Euclidean space, the axes cross a circle at right angles.

I think I really did mean "tangent [to the circle]",
where
the space-axis being "tangent to the circle"
defines
what "normal [to the worldline]" means.
I will add some words to my original statement for clarity:

The geometric reason for the tilting of the "space axes" is due to that space axis being parallel to the tangent to the "unit circle" ( a hyperbola in special relativity formed from the tips of the future unit-timelike vectors) at the event where that observer's 4-velocity meets the circle. This diagram (from the past thread I referenced...
https://www.physicsforums.com/threads/minkowski-diagram.876359/#post-5503686 ) should be useful.

https://www.desmos.com/calculator/ti58l2sair [my t axis is horizontal ]

 

[Orodruin]

I think I really did mean "tangent [to the circle]",
where
the space-axis being "tangent to the circle"
defines
what "normal [to the worldline]" means.
I will add some words to my original statement for clarity:

The geometric reason for the tilting of the "space axes" is due to that space axis being parallel to the tangent to the "unit circle" ( a hyperbola in special relativity formed from the tips of the future unit-timelike vectors) at the event where that observer's 4-velocity meets the circle. This diagram (from the past thread I referenced...
https://www.physicsforums.com/threads/minkowski-diagram.876359/#post-5503686 ) should be useful.

That really looks like the spatial axis being normal to the hyperbola ...

 

[robphy]

That really looks like the spatial axis being normal to the hyperbola ...

In that diagram, it is noted that my t-axis is horizontal... and the future-"circle" (whose events are timelike related to the origin) is shown in the right half. The worldline through the origin meets the hyperbola at an event. At that event, the tangent line to the circle is drawn. That tangent line to the circle is declared to be "normal" to the worldline [thought of as a radius vector].

This is in line with Minkowski, "Space and Time" p. 84-85

We divide up any vector we choose, e.g. that from O to x, y, z, t, into the four components x, y, z, t.
If the directions of two vectors are, respectively,
that of a radius vector OR from O to one of the surfaces (+/-) F = 1,
and that of a tangent RS at the point R of the same surface,
the vectors are said to be normal to one another.

In the context of my diagram,
the "F=1"-surface is my future-"circle" centered at O,
"OR" is the future-unit-timelike vector of the observer, where R is on that circle.
Then the tangent "RS" is normal to "OR" (along the observer's time axis).
Thus, the observer's space axis at event O will be defined as the parallel to this tangent-"RS"-to-the-circle drawn through the origin O.

 

[Orodruin]

In that diagram, it is noted that my t-axis is horizontal...

Ok, so your spatial axis is the dashed line. Yes, this line is tangent to the hyperbola, but it is not the spatial axis used in the standard Lorentz transformation - that spatial axis is a normal line to the other hyperbola (the hyperbola that has space-like separated from the origin). I think it is less confusing to talk about the axes which the standard configuration of the Lorentz transform relate - just as it is easier to talk about just rotations in Euclidean space instead of rotations+translation to the circle.

 

[robphy]

Ok, so your spatial axis is the dashed line. Yes, this line is tangent to the hyperbola, but it is not the spatial axis used in the standard Lorentz transformation - that spatial axis is a normal line to the other hyperbola (the hyperbola that has space-like separated from the origin). I think it is less confusing to talk about the axes which the standard configuration of the Lorentz transform relate - just as it is easier to talk about just rotations in Euclidean space instead of rotations+translation to the circle.

Yes, the dashed line is that observer's spatial axis.

At a glance, it might be confusing. But I thought I was explicit about my construction and my conventions.

Pedagogically, I think my presentation is better because

• my "circle" (the hyperbola that is timelike separated from the origin) arises from an operational construction: an experiment starting at event O, where observers traveling with various velocities marked when (say) 1 second has elapsed on their watch since event O.
  
• Once this circle is determined, orthogonality (being "normal" or "perpendicular") to a radius vector (along an inertial observer's worldline) in this geometry is then defined by tangency to this circle.
  (Then the parallel to this tangent can be used to construct the spatial-axis through event O.)
  
• This construction works in the Minkowski and Galilean spacetime geometries and in Euclidean space (using odometers in the plane, with surveyors traveling in different spatial directions).
  
• In the desmos visualization ( https://www.desmos.com/calculator/ti58l2sair ), you can see this by tuning the signature of the metric by tuning the y-coefficient of the "circle". [Here, I didn't want x along the vertical.] I use the parametrization $t^2-Ey^2=1$, where $E=1,0,-1$ is Minkowski, Galilean, and Euclidean, respectively.
  
  Furthermore, by tuning the two velocities, you can see how the observers generally disagree on these tangent lines (that is, what each declares the "line of constant t=1" is, demonstrating the relativity of simultaneity for the Minkowski case and the absoluteness in the Galilean case).
• [I kept the t-axis horizontal so that we obtain the usual PHY 101 position-vs-time graph in the Galilean case (although most are unaware of this nonEuclidean geometry underlying the usual position-vs-time graph).]

From this viewpoint, the "hyperbola that is timelike separated from the origin" is physically more fundamental (i.e. more primitive)
than the "hyperbola that is spacelike separated from the origin" (which can then be derived later, if needed).