MigMRF
- 15
- 0
So I'm playing around with some water rockets and I'm trying to figure out how fast the exhaust velocity of the water is. I've had an experimental approach using high fps camera to record and analyse (using tracker) the exhaust velocity. I'm using a 0,5 l soda bottle with 0,085 L ; 0,135 ; L 0,185 L and 0,235 L water. So far I've found, that more water means less exhaust velocity (the pressure is exactly the same at 1,8 bar). This makes sense, because the acceleration of the water comes from the energy of the pressurized air.
However I've found, that a lot of people use the Bernoullis equation (rewritten) to calculate the exhaust velocity with the formula:
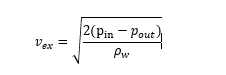
However there is no mass involved here?
However I've found, that a lot of people use the Bernoullis equation (rewritten) to calculate the exhaust velocity with the formula:
However there is no mass involved here?