Bernoulli’s Equation for plugging finger into dike under water

[member 731016]

Homework Statement

A legendary Dutch boy saved Holland by plugging a hole
of diameter 1.20 cm in a dike with his finger. If the hole was 2.00 m below the surface of the North Sea (density 1030 kg/m^3) (b) If he pulled his finger out of the hole, during what time interval would the released water fill 1 acre of land to a depth of 1 ft? Assume the hole remained constant in size.

Relevant Equations

Bernoulli’s Equation

For this part (b) of this problem

,
The solution is,

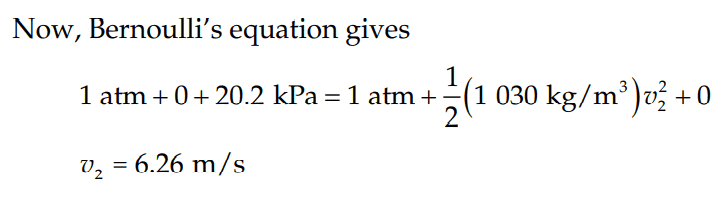
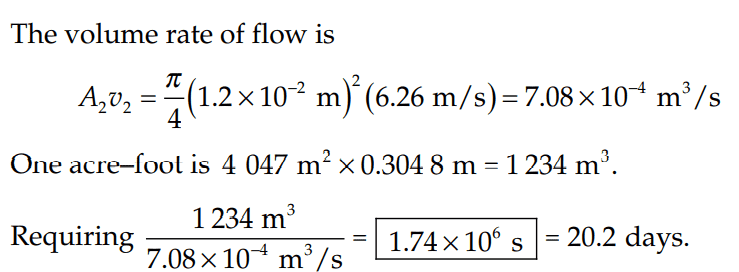
However, why are they allowed to assume for the Bernoulli's equation for the water outside the hole, that the water is stationary (i.e v_1 = 0)?

It also appears that they assume that the pressure inside the Holland is 1 atm, which is only valid when the water level is below the hole.

Many thanks!

 

[haruspex]

, why are they allowed to assume for the Bernoulli's equation for the water outside the hole, that the water is stationary (i.e v_1 = 0)?

On the sea side, I assume you mean.
You are right that immediately in front of the hole the water will be moving some, but also the pressure will have dropped a little in consequence. As you move a bit further back into the water, both of those effects diminish.
You could also forget about that region and instead consider the water surface. That certainly gives v₁=0, z₁=2m, p₁=atm.

 

[member 731016]

On the sea side, I assume you mean.
You are right that immediately in front of the hole the water will be moving some, but also the pressure will have dropped a little in consequence. As you move a bit further back into the water, both of those effects diminish.
You could also forget about that region and instead consider the water surface. That certainly gives v₁=0, z₁=2m, p₁=atm.

Thanks for your reply @haruspex ! I was assuming Holland was 2 m below the water as the problem says that. Were you assuming Holland was at sea level?

Is that why you said that I would be allowed to forget about that region and instead consider the water surface? The water surface is at 1 atm, while the region at the same height as the hole (2m below the surface) is at 1 atm + 20.2 kPa.

Many thanks!

 

[haruspex]

Were you assuming Holland was at sea level?

No.
In using Bernoull's principle you pick any two points in the 'streamline'. You have the exit point on the Holland side of the hole, but on the water side you do not have to choose a point right in front of the hole. For the reasons I gave, it is not entirely clear what the velocity and pressure are there. Instead, you can choose a point somewhat further away, on the same level, or a point on the surface. The first will give a pressure p_atm+gρz (z=2m) and a height difference zero, the second will give a pressure p_atm and a height difference z=2m. Either way, it adds up to the same.

 

[member 731016]

No.
In using Bernoull's principle you pick any two points in the 'streamline'. You have the exit point on the Holland side of the hole, but on the water side you do not have to choose a point right in front of the hole. For the reasons I gave, it is not entirely clear what the velocity and pressure are there. Instead, you can choose a point somewhat further away, on the same level, or a point on the surface. The first will give a pressure p_atm+gρz (z=2m) and a height difference zero, the second will give a pressure p_atm and a height difference z=2m. Either way, it adds up to the same.

Oooh thanks so much @haruspex , I understand now!