Biot-Savart Law For Calculating Net Magnetic Field

[Ignitia]

Homework Statement

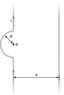
Two long wires, one of which has a semicircular bend of radius R, are positioned as shown in the accompanying figure. If both wires carry a current I, how far apart must their parallel sections be so that the net magnetic field at P is zero? Does the current in the straight wire flow up or down?

Homework Equations

[/B]
Vector of Magnetic Field:

B = μ_{o ^{/4π ∫ I * (dL X rΛ) / r}2}

rΛ is a vector. (no symbol available for it)

Magnitude of Magnetic Field:
B = (μ_o/4π) ∫ I*R*dθ/R²

μ_o = 4π*10^-7 T * m/A

The Attempt at a Solution

Okay, since wires have a 'parallel' parts, they cancel out, leaving only the semicircle and second wire needed to be calculated. Current on 1st wire heads upward, so Right Hand Rule indicates the field going inward at P from the semicircle. To cancel out, the field on the straight wire has to go outward - right hand rule says I should be upward as well. (Correct?)

B for semicircle:
B = (μ_o/4π) ∫ I*R*dθ/R²
B = (I*μ_o/4π)/R ∫dθ

∫dθ = π

so: B = (I*μ_o/4π)/R

Now I have to find -B with respect of the second current I with r = a, and add them together to get the answer.

B = (μ_o/4π) ∫ I*a*dθ/a²
B = (I*μ_o/4π)/R ∫dθ

∫dθ = 0

Meaning B = 0, which I know is not correct. Help?

 

[BvU]

I should be upward as well. (Correct?)

Seems OK to me

of the second current I with r = a

What is the B field from an infinite straight current carrying wire ?

 

[kuruman]

B = (I*μ_o/4π)/R ∫dθ

∫dθ = π

so: B = (I*μ_o/4π)/R

The π in the denominator of the last equation cancels with the π from the integral.

 

[Ignitia]

The π in the denominator of the last equation cancels with the π from the integral.

Woops, missed that. Thanks.

Seems OK to me
What is the B field from an infinite straight current carrying wire ?

okay, got it. Infinite wire simplifies to B = μ₀ * I / 2πa

So B1 - B2

μ₀ * I / 4R - μ₀ * I / 2πa = 0

μ₀ * I / 4R = μ₀ * I / 2πa

4R = 2πa

2R/π = a

Thanks!