Yankel
- 390
- 0
Hello all,
I have this question I struggle with...
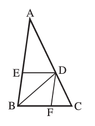
View attachment 7836
EDFB is a parallelogram. It is known that AB/BC = AD/DC.
1) Prove that the parallelogram is a rhombus.
2) It is given that: AB=9, AC=10, BC=AD. Calculate the side of the rhombus.
I think I solved the first part. There is a theorem called the "bisector of an angle theorem" according to which if AB/BC = AD/DC then the line BD is a bisector of an angle of the angle B and then a parallelogram in which the diagonal is a bisector of an angle is a rhombus. Am I correct ?
I have a problem with the second part. I can't figure out how to solve it. The answer should be 3.6. I have tried the intercept theorem (or Thales' theorem), but couldn't figure it out.
Can you kindly assist to in the second part of the question ?
Thank you in advance !
I have this question I struggle with...
View attachment 7836
EDFB is a parallelogram. It is known that AB/BC = AD/DC.
1) Prove that the parallelogram is a rhombus.
2) It is given that: AB=9, AC=10, BC=AD. Calculate the side of the rhombus.
I think I solved the first part. There is a theorem called the "bisector of an angle theorem" according to which if AB/BC = AD/DC then the line BD is a bisector of an angle of the angle B and then a parallelogram in which the diagonal is a bisector of an angle is a rhombus. Am I correct ?
I have a problem with the second part. I can't figure out how to solve it. The answer should be 3.6. I have tried the intercept theorem (or Thales' theorem), but couldn't figure it out.
Can you kindly assist to in the second part of the question ?
Thank you in advance !