PiRsq
- 112
- 0
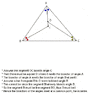
Prove that the bisectors of the angles of any triangle ABC are concurrent. The point of intersection is called the incentre, I.
Proof:
-Angle A and B are bisected and their bisectors meet at a point I
-Assume a line segment bisects angle C and meets the bisector of angle A at point O
-Assume a line from O to B that will bisect angle B
-But angle B is already bisected by segment BI
-So line segment OB must be BI
-Thus point O is I
-Therefore the incentre is at I
Does this proof workout?
Proof:
-Angle A and B are bisected and their bisectors meet at a point I
-Assume a line segment bisects angle C and meets the bisector of angle A at point O
-Assume a line from O to B that will bisect angle B
-But angle B is already bisected by segment BI
-So line segment OB must be BI
-Thus point O is I
-Therefore the incentre is at I
Does this proof workout?
Attachments
Last edited: