Gena
- 2
- 0
[Moderator's Note: Thread title changed to better reflect the problem statement]
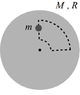
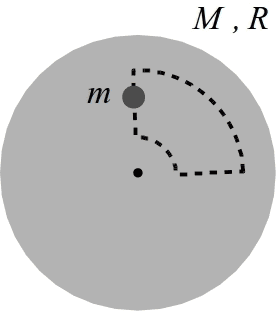
A body of mass m is on a disk of mass M=2m and radius R, initially static and free to spin around its center. The mass mm goes around a trajectory described in the image below with constant velocity v with respect to the platform. The circular arcs of the trajectory have a radium of R/4 and 3R/4 and an aperture of 90 degrees with respect to the disk.
After completing the trajectory, the mass stops.
What angle does the disk spin with respect to its original position?
Probably something related to conservation of the angular momentum or something, but honestly could be anything.
L=Iw
P=mv
no clue whatsoever on how to even approach this problem, any hint will be happily received. Thanks
Homework Statement
A body of mass m is on a disk of mass M=2m and radius R, initially static and free to spin around its center. The mass mm goes around a trajectory described in the image below with constant velocity v with respect to the platform. The circular arcs of the trajectory have a radium of R/4 and 3R/4 and an aperture of 90 degrees with respect to the disk.
After completing the trajectory, the mass stops.
What angle does the disk spin with respect to its original position?
Homework Equations
Probably something related to conservation of the angular momentum or something, but honestly could be anything.
L=Iw
P=mv
The Attempt at a Solution
no clue whatsoever on how to even approach this problem, any hint will be happily received. Thanks
Attachments
Last edited by a moderator: