Body sliding down an accelerating hemisphere

[chester20080]

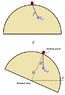
We have a frictionless hemisphere M,of a radius R and a body m on the top of it.We give to the hemisphere a horizontal constant acceleration W and consequently the body begins to slide down the accelerating hemisphere.What is the relative velocity of the body in respect to the hemisphere when the body leaves the hemisphere?And what is the angle θ that has made the body when it leaves the hemisphere,applying for W=g?
I thought that the faster the hemisphere moves forward, the faster the height of the body in y-axis reduces,so W=Ay,where Ay is the acceleration of the body in y-axis.The only acceleration of the body is the centripetal An,which breaks down to Ax and Ay for my convenience.So:Ay=W=>An*cosθ=W (1). Also: ΣFr=mAn=>mgcosθ-N=mAn (where N the normal reaction)<=>An=(mgcosθ-N)/m (2).From (1),(2):mgcosθ²-Ncosθ=mW.When the body leaves the hemisphere:N=0,so cosθ²=W/g=>cosθ=$\sqrt{W/g}$.But I also have:
An=u²/R =>W/cosθ=u²/R =>u²=gR$\sqrt{W/g}$ <=>
u=$\sqrt{gR\sqrt{W/g}}$.But that u is the velocity in respect to some motionless observer outside the system.To find the relative velocity we have to find and the velocity of the hemisphere the time the body leaves it.For the hemisphere:U_hsph=Wt and for the body:u_y=Ay*t=Wt.But u_y=ucos(π/2-θ)=>u_y=sinθ*u.So:
u_hsph=usinθ.
u_rltv=u-u_hsph(vectors) => u_rltv=sqrt{u²+u_hsph²}=>...=>u_rltv=$\sqrt{R*(2g-W)\sqrt{W/g}}$.
But the values for θ are just not normal,so I guess that the assumption Ay=W is wrong,right?
Can you tell me the principles that rule over the phenomenon (and the relative equations)?Any idea what to do?

 

[TSny]

In the inertial "lab" frame, the body does not move in a circle. So, I don't think you can say that the only acceleration the body has is centripetal acceleration in this frame of reference.

It might be much easier to switch to the frame of reference of the hemisphere. Are you familiar with the idea that in a reference frame that has uniform acceleration in a straight line, you can take into account the effect of the acceleration by just using a modified acceleration of gravity? That is, you can treat the reference frame of the hemisphere as an inertial reference frame if you modify the magnitude and direction of the acceleration of gravity.

 

[chester20080]

No,I haven't learned anything like that.Can you explain in further detail?And what is the orbit of the body m,why isn't it a part of a circle?

 

[TSny]

Suppose you are riding in a train that has a constant acceleration along a straight track.
In the inertial Earth frame you can apply Newton’s second law to the motion of a body:

$\sum{\vec{F}} = m\vec{a}$

You can write the acceleration of the body relative to the earth as a sum of the acceleration of the body relative to the train and the acceleration of the train relative to the earth:

$\vec{a} = \vec{a}_{b/t} + \vec{a}_{t/e}$

So, $\sum{\vec{F}} = m( \vec{a}_{b/t} + \vec{a}_{t/e})$

Rearrange:

$\sum{\vec{F}} - m\vec{a}_{t/e} = m\vec{a}_{b/t}$

So, the acceleration of the body relative to the train obeys the 2nd law if you include an extra “fictitious†force $- m\vec{a}_{t/e}$ acting on the body.

If you combine this extra force with the true force of gravity acing on the body, then you have

$m\vec{g}- m\vec{a}_{t/e} = m(\vec{g}- \vec{a}_{t/e} ) \equiv m\vec{g}_{\rm eff}$

So, Newton’s 2nd law will still hold in the train if you replace the true acceleration of gravity vector by a new effective acceleration of gravity vector

$\vec{g}_{\rm eff} \equiv \vec{g} - \vec{a}_{t/e}$

 

[TSny]

And what is the orbit of the body m,why isn't it a part of a circle?

In the frame of reference of the hemisphere, the body moves along a circular arc with increasing speed. But relative to the earth, the body has an additional horizontally accelerated motion. So, relative to the earth, the body does not move along a circle.

 

[chester20080]

But how does it get this horizontal acceleration,since no force acts towards the direction of the hemisphere on the body(no friction)?Is it from the normal force?Is it towards where the hemisphere is moving or from the opposite?And can you describe me precisely its exact orbit?Is it something like an ellipse?I just can't visualize it.

 

[TSny]

Yes, in the Earth frame the body gets it's horizontal acceleration, $a_x$, solely from the x-component of the normal force. By thinking about the direction of the normal force, you should be able to decide on the direction of the x-component of acceleration of the body relative to the earth.

I don't believe the precise trajectory relative to the Earth will be a simple curve like an ellipse or parabola. But if you draw a few sketches at different moments you should be able to see the rough shape of the trajectory relative to the earth.

 

[chester20080]

If I consider the hemisphere reference frame as you said then we have only centripetal acceleration for the body.So how do I combine this with what you mentioned above about the effective acceleration,since there is no horizontal acceleration for the body?The only thing that changes for my first post if we consider this frame of reference isn't that u is the relative velocity?

 

[TSny]

If I consider the hemisphere reference frame as you said then we have only centripetal acceleration for the body.So how do I combine this with what you mentioned above about the effective acceleration,since there is no horizontal acceleration for the body?The only thing that changes for my first post if we consider this frame of reference isn't that u is the relative velocity?

In the hemisphere frame, there will be both centripetal acceleration and tangential acceleration. It will be similar to the more familiar problem where you let a block slide down a hemisphere that is kept at rest. But, now you will need to use an effective acceleration of gravity $\vec{g}_{\rm eff} \equiv \vec{g} - \vec{a}_{hemisphere/earth}$

This means that the "force of gravity" $m\vec{g}_{\rm eff}$ will not be vertical and it will have a magnitude that differs from normal mg.

 

[chester20080]

By that you mean that wherever I have g I use instead of it the g_eff?And wherever I find u is the relative velocity?And I justify the use of g_eff by the explanation you said,despite the fact we haven't learned such a thing?

 

[TSny]

By that you mean that wherever I have g I use instead of it the g_eff?

Not just change the magnitude of g, but also the direction. Note that g_eff is found by vector addition of the true gravitational acceleration vector and the negative of the acceleration vector of the hemisphere (relative to the earth).

And wherever I find u is the relative velocity?

Yes, the velocity of the body in the hemisphere frame is the velocity of the body relative to the hemisphere.

And I justify the use of g_eff by the explanation you said,despite the fact we haven't learned such a thing?

Since I don't know what you have covered in your course, I don't know what method you are expected to use. Can you relate this problem to what you are currently studying in the course?

 

[TSny]

Note. The nice thing about using the effective g is that you can still use energy concepts just as you would do if the hemisphere is not allowed to move relative to the earth. But you do need to take into account the complication that $\vec{g}_{\rm eff}$ is no longer perpendicular to the ground.

 

[chester20080]

In our course we have just "touched" the relative motions,nothing any further in detail...So the body has two accelerations in this reference frame,centripetal and effective (with its direction) and using the equations for the centripetal acceleration and the conservation of energy we solve the problem in that way?

 

[TSny]

Yes. Relative to the hemisphere, the acceleration of the body can be broken down into centripetal and tangential components. As you say, you can use the centripetal component of F = ma and conservation of energy to solve the problem.

 

[chester20080]

Because I am confused about how to use practically g_eff,can you write me a few equations about the body,showing the usage of g_eff?

 

[TSny]

Because I am confused about how to use practically g_eff,can you write me a few equations about the body,showing the usage of g_eff?

Recall $\vec{g}_{\rm eff} = \vec{g} - \vec{a}_{hemisphere/earth}$.

See if you can write expressions for the magnitude and direction of $\vec{g}_{\rm eff}$ in terms of g and W.

 

[chester20080]

I think I got it.The relative velocity will be a function of the angle,right?Here is what I have found:
u_relative=$\sqrt{}(R(gcosθ-Wsinθ))$ and
cosθ(g+2sqrt{g²+W²})-Wsinθ-2sqrt{g²+W²}=0. If the latter one is right,how do I solve this? But thankfully,our professor said that the angle should be around 17 degrees for W=g,so I plugged this in the angle equation and I got 0.5...=0,which leads me to consider the equations to be right,because he said around 17 degrees,so we are almost there!What do you think?

 

[TSny]

The relative velocity will be a function of the angle,right?

Yes.

Here is what I have found:
u_relative=$\sqrt{}(R(gcosθ-Wsinθ))$ and
cosθ(g+2sqrt{g²+W²})-Wsinθ-2sqrt{g²+W²}=0.

Check to see if these two equations make sense at θ = 0?

 

[chester20080]

What,do you think they are wrong?

 

[TSny]

Take your equation u_relative=$\sqrt{}(R(gcosθ-Wsinθ))$.

What does this give you for u_relative when θ = 0?

 

[chester20080]

u_relative=$\sqrt{}gR$

 

[TSny]

Does this make sense? What should the relative speed be when θ = 0?

 

[chester20080]

Zero.Yep,I hurried...In the energy conservation,as initial potential energy,what do I have? m(R-Rcosθ)*g_effy or ...*g_eff?

 

[TSny]

It might help to have a diagram. Let's suppose the hemisphere accelerates to the left relative to the Earth so that the body slides down the right side of the hemisphere. In the frame of reference of the hemisphere you replace $\vec{g}$ by $\vec{g}_{\rm eff}$ which is directed at some angle β as shown in the top diagram.

I found it helpful to rotate the top diagram to have a diagram in which $\vec{g}_{\rm eff}$ is vertical.

 

[chester20080]

So you say to consider the rotated form and to solve the problem just like when the hemisphere is motionless and to use instead of mg, mg_eff?If so,how do we know the angle the body leaves the hemisphere isn't included in the initial angle we rotated the system;I mean how do we know the body after the "rotation" is still on the hemisphere and leaves it some time later?Won't we have to consider some constraints in that way (which I have to admit it helps)?

 

[TSny]

In the rotated diagram, the body starts from rest at θ = β. As long as β < 90^o, the body will have to slide a finite distance along the spherical surface before it falls off.

 

[chester20080]

What if,for instance,β=10 degrees and the body normally falls off at 5?

 

[TSny]

Suppose in the lower diagram β = 10^o. Then the block would have to fall off at an angle θ > β in the lower diagram, say θ = 15^o. What would this mean in terms of the angle θ that the block falls off in the upper diagram?

 

[chester20080]

That normally falls off at 5 degrees and there is no problem.But what if it would have fallen off for θ<β?Anyway,if we don't rotate it,then the y-component of g_eff (perpendicular to the ground)would be g,so in the equation of the energy conservation we would have mgeffyh=mgh.Or not?

 

[TSny]

That normally falls off at 5 degrees and there is no problem.But what if it would have fallen off for θ<β?

In the lower diagram, β is the value of θ at which the body starts at rest. It won't fall off until it has traveled at least some distance. So, the body must move through some angle Δθ before falling off. That means that the body must travel through the same change in angle Δθ in the upper diagram before falling off.

Anyway,if we don't rotate it,then the y-component of g_eff (perpendicular to the ground)would be g,so in the equation of the energy conservation we would have mgeffyh=mgh.Or not?

The magnitude of the change in potential energy due to g_eff is mg_effd where d is the distance the body moves parallel to $\vec{g}_{\rm eff}$. In the lower diagram, d is just |Δy'|.

 

[chester20080]

So in the occasion where we don't rotate the system,the initial potential energy would be mg_effd, d would be what?

 

[TSny]

I probably should use a prime on θ to denote the angle from the y' axis in the rotated figure. So, in the rotated figure, the body starts at θ' = β, which corresponds to θ = 0 in the top figure. In the rotated figure, the body falls off for some θ' > β, which means it falls off for some θ > 0 in the upper figure.

 

[TSny]

So in the occasion where we don't rotate the system,the initial potential energy would be mg_effd, d would be what?

Draw a figure showing the initial position and final position of the block (where it leaves the surface). Draw a vector between these two positions. This is the displacement vector Δr of the body. d is the component of Δr in the direction of g_eff.

 

[chester20080]

I think I found an equation for the relative velocity,considering the rotated system as you advised me to.I have:
u_relative=$\sqrt{}2R(g-gcosθ+Wsinθ)$. It yields Urelative=0 for θ=0.

 

[TSny]

I think I found an equation for the relative velocity,considering the rotated system as you advised me to.I have:
u_relative=$\sqrt{}2(g-gcosθ+Wsinθ)$. It yields Urelative=0 for θ=0.

Except for a missing R that looks good!