kidsasd987
- 142
- 4
Hello, I have a question about Boltzmann Distribution.
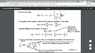
I wonder why partial N of Nj is 1 and partial U of Nj=Ej. because N is constant, partial N of Nj has to be 0 and Partial Nj of U has to be 0 as well.
They are constants so, to make sense of the equation, alpha and beta have to be 0 but this is still absurd.
Can anyone tell me why this is true?
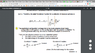
I wonder why partial N of Nj is 1 and partial U of Nj=Ej. because N is constant, partial N of Nj has to be 0 and Partial Nj of U has to be 0 as well.
They are constants so, to make sense of the equation, alpha and beta have to be 0 but this is still absurd.
Can anyone tell me why this is true?