kinnabird5
- 6
- 0
My teacher gave this problem to my class, for anyone who was failing, only one person was able to solve it correctly. It has been driving me crazy for almost two years. Alot of peolpe have said that it is impossible, but I assure you it is not. It was solved by a 17yr old student. here is the best I can explain it, without drawing it actually.
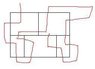
Imagine a rectangle that has a split line horizontaly through the middle. On the top half of the rectangle is a line that is verticle, in the center, connecting the first and second horizontal lines. Now on the bottom half of the rectangle, there are two verticle lines, connecting the second and third horizontal lines, one vertical line on either side of the top verticle. So in all, it should appear to be a large rectangle with two small rectanles on top of three smaller rectangles. Simply five in one.
Now you must draw a line through each line, or sides, of all reactangles. There are 16 sides in all. The line cannot break, fork, or overlap. The line cannot pass through the same side twice.
Please email me if this confusses you and i can email you the picture back. Thank you for your help!
Imagine a rectangle that has a split line horizontaly through the middle. On the top half of the rectangle is a line that is verticle, in the center, connecting the first and second horizontal lines. Now on the bottom half of the rectangle, there are two verticle lines, connecting the second and third horizontal lines, one vertical line on either side of the top verticle. So in all, it should appear to be a large rectangle with two small rectanles on top of three smaller rectangles. Simply five in one.
Now you must draw a line through each line, or sides, of all reactangles. There are 16 sides in all. The line cannot break, fork, or overlap. The line cannot pass through the same side twice.
Please email me if this confusses you and i can email you the picture back. Thank you for your help!