Calculate Force Req. to Lift Load 3m High

[kalpesh]

I want to know how to calculate the amount of force req. in the given picture. I want to lift the load 3 meters high.

Can anyone help.

 

[Chen]

Where is the picture?

 

[kalpesh]

I attached it in the thread
Dont know how to use it

Thanks

Kalpesh

 

[Chen]

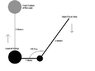
I can't see how you can lift the load 3 meters high when the lever connected to it is just 1 meter long. Or do you mean "throwing" the load 3 meters high, rather than lifting it while it's on the lever?

 

[kalpesh]

You got it right my friend

The ball / load is not attached to the arm.

Hence the ball needs to be thrown upwards.

 

[Michael D. Sewell]

kalpesh,
You have given us a point of application, but no direction or sense.
-Mike

 

[kalpesh]

Michal

I have changed the image for your ref.

please help me how to calculate the req. force whith the given angle and also if you change the angle.

Kalpesh

 

[turin]

You need to apply energy, not force (they are related, but it will be easier to first consider the required energy, and then translate that into how much force to apply).

 

[kalpesh]

Thanks TURIN

But in that case u will need to tell me how to find energy and then how to convert it to force.

Thanks
Kalpesh

 

[Chen]

Generally speaking, the work done by all non-conservative forces is equal to the change in mechanical energy of the object. In your case:

{W_F}_{ext} = \Delta E_m = \Delta E_k + \Delta E_p

Since the inital velocity and final velocity are both zero, there is no change in kinetic energy so it comes down to this:

W_F = \vec F\cdot \vec x = mgh

 

[turin]

And don't forget that the x vector has a maximum value (determined by the lever arm).