Petrus
- 702
- 0
Calculate limit
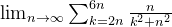
I have none progress, Is there any special rule for this limit?
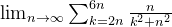
I have none progress, Is there any special rule for this limit?
