Calculate the height of a water column and expressions for P

[Richie Smash]

Homework Statement

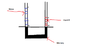
The apparatus shown may be used to determine the density of an unknown liquid X.
The tube has a uniform cross section and the height of the water column is twice that of Liquid X.
A and B are the same horizontal level. The pressure difference between points A and C is 2.5*10³Pa.

(i) Calculate the height of the water column.
(ii) Express P_B-P_D in terms of P_A and P_C
[Hint: the answer can be deduced without resorting to any further calculation]
(iii)What is the relationship between P_Cand P_D?
(Density of water = 1000 kg m^-3; g = 10 m/s)

Homework Equations

Pressure =ρgh

The Attempt at a Solution

Well I know the pressure at A would be : P=ρgh and in this case the height would be the water column's height as A is at the bottom.

But they do not give me a pressure, only a pressure difference...

I could write, P=pghA+pghB...
I'm stuck i think.

 

[Richie Smash]

Actually I did this, Pressure difference= pghA-pghC

and actually since hA-hC is the height itself, this can simply be rewritten as

2.5*10³= pgh
And now I can substitute in my values for density and gravity that were given and got 0.25m is the height of the column.

I'm hoping this is correct but for parts (ii) and (iii) I'm not entirely sure.

 

[Alloymouse]

Yes, since g and rho (density) are constants, you are right to just cancel them out on LHS and RHS.

And also, since only the atmosphere is "pushing down" on points D and C, they experience about the same pressure. Hence Pc = Pd

 

[Richie Smash]

I'm not entirely sure that's what they are asking for, because they ask write it in terms of Pa and Pc and Since D is lower than C, I don't think they are equal...

If Pa-Pc= pghA-pghC
then since the other column is half of that,
My best guess for an expression would be : (pghA)/2-(pghC)/2
= pgh_water/2

can anyone confirm this??

 

[Alloymouse]

notice that they are different liquids; you cannot compare based on height alone if both liquids are different in density :) if the pressures are different at D and C, then the side of higher pressure will naturally be pushed down until there is an equilibrium. Forces must be in equilibrium.

 

[Richie Smash]

Oh yes I understand what you mean so I know the answer for part (iii) .

But I still don't know if part (i) was correct and I don't know how to write part (ii) Pd-Pb in terms of Pa and Pc...

 

[Alloymouse]

Yes, your part (i) is correct;

so now you know that since A and C are the same height, they are at the same pressure, since the level of mercury on either side is the same (so no force "imbalance"). Since you understand now that B and D are the same pressure, you can express all of these in pressure.

 

[Richie Smash]

Umm I'm still not entirely sure on this, you are saying that the pressure of both liquids is the same, because the mercury level is constant?

 

[Alloymouse]

Umm I'm still not entirely sure on this, you are saying that the pressure of both liquids is the same, because the mercury level is constant?

Yes. If the pressure at those points are not equal, the mercury level will be higher on one side to "compensate"

 

[Richie Smash]

Right I'm following up to this point, but this is my reasoning , if atmospheric pressure decreases as you go higher, and increases as you go lower, why is the atmospheric pressure at D and C the same if one is lower? Sorry this is my weakest area in physics I really struggle with pressure

 

[Alloymouse]

Right I'm following up to this point, but this is my reasoning , if atmospheric pressure decreases as you go higher, and increases as you go lower, why is the atmospheric pressure at D and C the same if one is lower? Sorry this is my weakest area in physics I really struggle with pressure

Ah! The thing is, at such a small height difference, we ignore the difference in atmospheric pressure since it is rather insignificant. We will take this into account when your setup is absolutely massive (think about the size of a mountain). Otherwise, there is no need to worry as air is really not that dense to matter for pressure here.

 

[Richie Smash]

ok but I'm still confused as to this part.
They're asking for an algebraic expression of Pb-Pd in terms of Pa-Pc

I know that : Pa -Pc = pghA-pghC= 2.5x10³Pa

If so the expression would be pg (hA)/2-pg (hB)/2 = 2.5x10³Pa? =Pb-Pd

 

[Alloymouse]

ok but I'm still confused as to this part.
They're asking for an algebraic expression of Pb-Pd in terms of Pa-Pc

I know that : Pa -Pc = pghA-pghC= 2.5x10³Pa

If so the expression would be pg (hA)/2-pg (hB)/2 = 2.5x10³Pa? =Pb-Pd

Don't worry, let's take it slow.

You know that pressure at A = pressure at B

You also know that pressure at C = pressure at D

Hence,
Pa = Pb

Pc = Pd

Hope this can give you a hint ;)

 

[Richie Smash]

Ok I just realized something, I have to find a way to get density out of the equation to express this, because the density of the water and density of liquid X are note the same.

 

[Alloymouse]

Ok I just realized something, I have to find a way to get density out of the equation to express this, because the density of the water and density of liquid X are note the same.

Here's another hint:

The heights are different too! So my suggestion is that since you know that pressures at a couple of points are equivalent, you could sub them in directly

 

[Richie Smash]

so basically Pa-Pc= Pb-Pd?

I guess it's right but I thought it wuld have been more to it

 

[Alloymouse]

so basically Pa-Pc= Pb-Pd?

I guess it's right but I thought it wuld have been more to it

Bingo! Fortunately, some problems have solutions simpler than expected :)