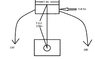
First, to size a motor, you must define how much power you need. Let's do a simplified analysis.
The power is defined by the torque times the angular velocity. The maximum torque needed will be when the pole is horizontal at 162 lb.ft or 220 N.m. It will decrease at it goes up. The average speed is 1 deg/s or 0.0175 rad/s. Therefore, assuming you've reach the average speed instantly, the maximum power would be:
$$220\ N.m \times 0.0175\ rad/s = 3.85 W$$
So you need a motor than can produce about 4 W. But is it reasonable to assume that the average speed would be reached almost instantaneously?
Let's assume we want to reach the average speed within 1 deg of rotation or 0.0175 rad. So the constant acceleration needed is (as
@CWatters showed how):
$$\frac{(0.0175\ rad/s)^2}{2 \times 0.0175\ rad}= 0.00875\ rad/s^2$$
With the corrected mass moment of inertia (1/3 instead of 1/12) as calculated by
@CWatters, i.e. 48.6 kg.m², you can find the extra torque needed to accelerate the pole to its average speed within 1 deg of rotation:
$$48.6\ kg.m^2 \times 0.00875\ rad/s^2 = 0.43\ N.m$$
Which is a ridiculous amount compared to the 220 N.m that your motor is already producing to hold the pole. So it is OK to assume that you will reach your average speed almost instantaneously with such a motor.