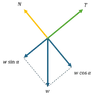Calculating acceleration of a prism and block connected to a wall through a rope and pulley

[Patrick Herp]

Homework Statement

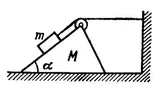
The figure shows a block of mass m above a prism of mass M with a slope α. The block is connected to the wall through a massless rope and pulley system. Assume all surfaces are smooth. Determine the acceleration of prism M with respect to the ground.

Relevant Equations

$$
\sum{F} = ma
$$

The figure shows a block of mass m above a prism of mass M with a slope α. The block is connected to the wall through a massless rope and pulley system. Assume all surfaces are smooth. Determine the acceleration of prism M with respect to the ground.
(Figure is the last attached image)

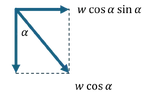
I can draw the force diagram on block m like the first attached image, but I'm not sure about my force diagram for prism M (second attached image). If that's true, then I think the prism acceleration should be:
$$
a_x = \frac{F_x}{M} = \frac{mg \sin{\alpha} \cos{\alpha}}{M} = \frac{m}{M} g\sin{\alpha} \cos{\alpha}
$$
The thing is, I don't know how to justify my force diagram on the prism. Is the contact force on the prism from the block really $mg \sin{\alpha} \cos{\alpha}$?

 

[haruspex]

I take it that where you have three arrows in the same colour, two of them are the third resolved into components parallel and normal to the slope.
There are more forces on the prism.
With only the force shown, why doesn’t the prism descend?
What keeps the rope bent?
Wrt the contact force from the block, remember that the block is accelerating too.

 

[Patrick Herp]

Wrt the contact force from the block, remember that the block is accelerating too.

Well, I'll try.
Assuming the rest reference frame of the floor, if I set the "downhill" acceleration of the block relative to the prism as $a_b$ while the acceleration of the prism as $a$, then Newton's 2nd law on the block perpendicular to the inclined plane is $$
N - mg \cos{\alpha} = ma \sin{\alpha}
$$ Meanwhile, along the inclined plane: $$
T - mg \sin{alpha} = ma \cos{\alpha} - a_b
$$
As for the prism, Newton's 2nd law along the x-axis (parallel to the floor) is: $$
N \sin{\alpha} = Ma
$$ However, I'm still left with T, and I don't think using Newton's 2nd law for the prism along the y-axis is going to help (not that I'm sure this one is correct): $$
N \cos{\alpha} + Mg = N_{pf}
$$
Now, I've been looking up solutions online, and I found a useful constraint; the length of the rope is constant, meaning the total rope length on the left side of the pulley (let's say l1) and its right side (say, l2) should be constant: $$
\begin{align}
l_1 + l_2 &= l \nonumber \\
\frac{dl_1}{dt} + \frac{dl_2}{dt} &= 0 \nonumber \\
a_b - a &= 0 \nonumber
\end{align}
$$
I've been thinking of using Newton's 2nd law on the block and the prism as a system, but I'm not sure how. Can I put $T$ on the right side of the pulley as an external force that works on the system?

 

[haruspex]

Well, I'll try.
Assuming the rest reference frame of the floor, if I set the "downhill" acceleration of the block relative to the prism as $a_b$ while the acceleration of the prism as $a$, then Newton's 2nd law on the block perpendicular to the inclined plane is $$
N - mg \cos{\alpha} = ma \sin{\alpha}
$$

Which way are you taking as positive for a?

Meanwhile, along the inclined plane: $$
T - mg \sin{alpha} = ma \cos{\alpha} - a_b
$$
As for the prism, Newton's 2nd law along the x-axis (parallel to the floor) is: $$
N \sin{\alpha} = Ma
$$ However, I'm still left with T,

As I asked in post #2, what is keeping the rope from straightening?

 

[haruspex]

Well, I'll try.
Assuming the rest reference frame of the floor, if I set the "downhill" acceleration of the block relative to the prism as $a_b$ while the acceleration of the prism as $a$, then Newton's 2nd law on the block perpendicular to the inclined plane is $$
N - mg \cos{\alpha} = ma \sin{\alpha}
$$

Which way are you taking as positive for a?

Meanwhile, along the inclined plane: $$
T - mg \sin{alpha} = ma \cos{\alpha} - a_b
$$
As for the prism, Newton's 2nd law along the x-axis (parallel to the floor) is: $$
N \sin{\alpha} = Ma
$$ However, I'm still left with T,

As I asked in post #2, what is keeping the rope from straightening?