Calculating Angle to Shoot Sword Over Wall for UT - 65 Characters

[Superman123]

Homework Statement

UT has jumped over a wall and unfortunately for her, she forgot to bring her sword. Her friend SS decided to shoot the sword to her with a bow. He can bend a bow and arrow so that it gets a potential energy of 179 Nm. It seemed that Ut landed 9 meters behind the wall; a house was standing in the way. We know that the wall is 14 meters high. So, from which angle must SS shoot the arrow so that UT receives her sword quietly in her hands? ( Both Ut and her hand will be 2.4 meters above ground when she receives the sword, the sword weighs 1280 grams). Do we need more assumptions to solve the problem?

Homework Equations

W= mgh

The Attempt at a Solution

I started by calculating how much energy that was needed to get the sword to the top of the wall.
W= 1.28 kg * 9.82 *14 = 176 Nm. He can bend the bow with a 179 Nm potential, that means he can get it over to the wall.

I couldn't figure out more than this, don't really understand how get the right angle and what other assumptions might be.

 

[Superman123]

Could other assumptions be the length of UT and SS?

 

[haruspex]

Could other assumptions be the length of UT and SS?

You are given the height at which UT is to catch the sword, but not the height it is fired from.

how much energy that was needed to get the sword to the top of the wall.

That doesn't help much. If all the energy were used merely getting it there then there would no KE left to propel the sword the remaining horizontal 9m.

You have to start by assigning some variable names to unknowns. We might be able to eliminate these later.
What extra parameters do you need in order to deduce the trajectory?

 

[Superman123]

Well, if we suppose that SS height when he realizes the bow is 2.6 meters. That would help us in reducing the work needed to get the sword to the top of the wall (143 Nm). Still, as you've said, the energy left(36 Nm) is not enough for the 9 horizontal meters.
The first unknown variable is the angle from which the sword should be shot. we can call it . Other variables might be how far SS should stand away from the wall, β. I am not sure, but if he is standing in the right position, it might reduce the work needed.

Is there a specific equation that might help with reducing the trajectory?

 

[haruspex]

the energy left(36 Nm) is not enough for the 9 horizontal meters.

Are you sure? How did you deduce that?

The first unknown variable is the angle from which the sword should be shot. we can call it . Other variables might be how far SS should stand away from the wall, β. I am not sure, but if he is standing in the right position, it might reduce the work needed.

Good.

Is there a specific equation that might help with reducing the trajectory?

Just find an equation for the velocity needed, given the extra unknowns you introduced, then optimise.

 

[Superman123]

I could deduce the energy by subtracting the height that assumed the height of SS when he shoots the bow(2.6). 14-2.6= 11.4 meters
W= 11.4*9.82*1.28≈143 , 179-143= 36 Nm left.

About formulae. Well there is vf2 = vi2 + 2*a•d and
vfy2 = viy2 + 2*ay•y . One problem I have is how to progress with them. I know d (2.6) I know vi2 (0), but if I am unsure if they're the right ones or if I am using them correctly. What formula do you suggest?

 

[haruspex]

I could deduce the energy by subtracting the height that assumed the height of SS when he shoots the bow(2.6). 14-2.6= 11.4 meters
W= 11.4*9.82*1.28≈143 , 179-143= 36 Nm left.

About formulae. Well there is vf2 = vi2 + 2*a•d and
vfy2 = viy2 + 2*ay•y . One problem I have is how to progress with them. I know d (2.6) I know vi2 (0), but if I am unsure if they're the right ones or if I am using them correctly. What formula do you suggest?

You have to consider the horizontal motion. And don't plug in any numbers yet... much better to work purely symbolically.

If the launch velocity is v at angle θ to the horizontal, what are the horizontal and vertical components?
Let the top of the wall be y₁ above the launch point, horizontally x₁ from the launch point, and suppose it takes time t₁ to just scrape by it. What two equations can you write relating these five variables?

 

[Superman123]

I can start by figuring out the vertical and horizontal components. If V is the launch velocity, then the vertical component is V, and the horizontal is Vx. If so, then the first equation might be the angle θ, which would be tan θ = Vy/Vx. Another equation related to this is V^2 = Vx^2 + Vy^2.
I guess from that information and with the help of my physics book, ΔX= X1- X0 and ΔY=y1-y ⇔ ΔY= v* t1 * cos θ

The equations:
ΔX= v* t1 * cos θ
tan θ = Vy/Vx
Are those the equations that you were looking for or are there other ones that could help out more with this case?

 

[haruspex]

ΔX= v* t1 * cos θ

Yes, but what does ΔX represent here, given the meaning of t1?

ΔY= v* t1 * cos θ

You do not mean cos here, and what about gravity? Are you familiar with the SUVAT equations for uniform acceleration?

 

[Superman123]

By ΔX, I meant the whole span of the projectile. If it goes from X1 to X0. I thought gravity could be incorporated in ΔY, in some weird way.

I don't really know that much about the SUVAT equations, but I've worked with them many times.

 

[haruspex]

By ΔX, I meant the whole span of the projectile.

As I suggested, break it into two phases: from launch to top of wall and from there to catch.
Create distinct variables for each phase.

I thought gravity could be incorporated in ΔY, in some weird way.

I don't really know that much about the SUVAT equations, but I've worked with them many times.

https://en.wikipedia.org/wiki/Equations_of_motion#Uniform_acceleration

 

[Superman123]

I thought about the question a couple of days, divided the question into two parts.
https://docs.google.com/drawings/u/0/d/sTkjl4n0fjD-E95twuL050A/image?w=482&h=357&rev=36&ac=1https://docs.google.com/drawings/u/0/d/sRt3xYoSFQaMvop31aaJVqA/image?w=465&h=423&rev=22&ac=1

My phys. teacher told that I was making it more complicated than it should be. I will of course try to continue to working with this method but is there an easier way to solve it?

 

[haruspex]

I thought about the question a couple of days, divided the question into two parts.
https://docs.google.com/drawings/u/0/d/sTkjl4n0fjD-E95twuL050A/image?w=482&h=357&rev=36&ac=1https://docs.google.com/drawings/u/0/d/sRt3xYoSFQaMvop31aaJVqA/image?w=465&h=423&rev=22&ac=1

My phys. teacher told that I was making it more complicated than it should be. I will of course try to continue to working with this method but is there an easier way to solve it?

Your images don't work for me.
Perhaps your physics teacher is assuming that the least speed is needed if clearing the wall is at the highest point of the trajectory. That might be true but it is far from obvious. Although standing a little closer to the wall, so that the highest point is a bit beyond the wall, requires a greater vertical velocity it needs a lower horizontal velocity. One can imagine that might be a lower speed overall.

 

[haruspex]

I tried a simple example. Wall height 1, distance beyond wall to target = 4, g=9.81. Launch and land at height 0.

Using the naive (symmetric) solution of launching from distance 4 in front of the wall, so that peak height is at the wall, gives
Launch angle = 26.6 degrees, launch speed = 9.9m/s.
A better solution is to stand much closer, distance 0.96m.
Launch angle = 52.0 degrees, launch speed = 7.1m/s.

In general, if the wall is height h and the distance beyond the wall is d then the optimal angle is (π-atan(d/h))/2, while the naive solution is atan(2h/d).

So unless your physics teacher has some very clever method, I do not see that there is a much easier way than the two-stage analysis.

That said, for the problem as given, the difference turns out to be quite small. The naive solution gives 16.18m/s, while the optimal solution gives 16.06m/s. The larger the ratio of horizontal to vertical the greater the benefit of the optimal solution.

 

[Superman123]

I misunderstood the question, the axe is thrown from a height of 2.4 meters and also received from a height of 2.4 meters behind the wall. Thinking of it as a quadratic equation. If she receives the sword from a point (9. 2,4), if the y-axis is the wall; then her friend throwing the axe will also be standing 9 meters behind the wall.
I saw your solution, I sort of understand it. My teacher showed something similar, my only problem is how do you receive the velocity?

 

[Superman123]

I tried to solve it by calculating the time first by using the equation s=v0t+((at^2)/2)), V0= 0. If the guy can make the sword have a 179 NM potential energy. I thought that if divided that by 18, the distance, I will have the acceleration. 179/18≈9.95 m/s
s=18
a=9.95

18=(9.95*t^2)/2
t≈1.9 s

v=v0+at= 0+9.95*t1.9 ≈ 18.9 m/s

 

[Superman123]

About the optimal angle and (π-atan(d/h))/2. Does that mean the angle should be, (pi-arctan(9/11.6))/2=-17?

 

[haruspex]

if the y-axis is the wall

But there is no reason to suppose that is optimal. Imagine a low wall with the receiver a long way from it. If the high point of the trajectory is the top of the wall then the thrower will be a long way from the wall also and will have to throw very hard. Obviously it would better in that case to throw from much closer to the wall.

I saw your solution, I sort of understand it. My teacher showed something similar,

I did not post the method, beyond saying to break it into two stages, so I'm not sure what there was to understand.
In what way is your teacher's solution similar? That does not seem to fit with your earlier statement that your teacher said my method (or your implementation of it) was unnecessarily complicated.

179 NM potential energy. I thought that if divided that by 18, the distance, I will have the acceleration.

Sounds like just a wild guess to me. Is there some reasoning behind that?

Does that mean the angle should be, (pi-arctan(9/11.6))/2

Yes.

=-17

No. How do you get that, and what units is it in? The expression gives me 1.24 radians, or 71 degrees.

 

[Superman123]

My teach. gave a formula that could be used, just like you did. His was θ=arctan((v^2)/g*Δx)-√((v^2(v^2−2gΔy))/(g^2*Δx)−1 )). To use it, I needed figure out the velocity. To figure out the velocity using suvat, I needed the acceleration, but as you said It was a wild guess. I needed to use f=ma, I know F=179/18=9.5
9.5=1.28*a
a=7.42

t= 1.22 sec
v= 9.05 m/s

I had done the wrong calculation, I also got 71.1 degrees as the answer to (pi-arctan(9/11.6))/2. I don't understand how you could figure out the angle with just (pi-arctan(9/11.6))/2 without taking into account the mass of the object or the acceleration or you may have don't, but in a different way.

 

[haruspex]

F=179/18

Try to understand what you are saying with that equation. You are taking the energy stored in the bow and dividing by the presumed (I'll come back to that) horizontal distance of travel, 18m, to obtain a force. What force would be calculated by that? It is the force which would provide that energy if applied over a distance of 18m. There is no force in this scenario which is being applied constantly over 18m, so it is a competely bogus calculation.

The 18m distance ASSUMES that the thrower should stand the same distance in front of the wall as the receiver is behind it. I.e. that the highest point of the trajectory is directly above the wall. This is what I have been calling the naive solution. You get away with it in the scenario given because in the two distances given, the height, 14-2.4m, is greater than the distance beyond the wall, 9m. This means it will turn out that standing 9m in front will be close to the best (where best means requiring the least energy). And it turns out that the given energy of 179J is enough. If the given energy were somewhat less (I've not worked out exactly how much less), this naive solution would say there is not enough energy to get there, whereas in the ideal solution I provided, standing a bit closer, there might be enough.
If I could get to speak to your teacher I would admonish him for not specifying that the thrower should stand 9m in front. He is creating the impression that this is always a valid assumption. If you were to cut the wall height to, say, 4.4m, it would become painfully obvious that standing 9m from the wall to throw the sword is silly.

So, setting that aside, your question now is how to find the velocity needed for the naive solution.
You know the PE stored in the bow. That, we assume, is all turned into KE of the sword. If the sword has mass m and speed v at launch, what is its KE in terms of m and v?

Finally, having assumed the thrower and receiver are equidistant from the wall, you should know how to obtain the formula for the angle. Here are the steps:
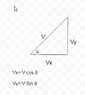
If the throw speed is v and the angle is θ, what are the horizontal and vertical components?
If the height to be cleared is h (=14-2.4m, but just leave it as unknown h in answering), with that vertical velocity, how long will it take to reach its maximum height? Get an equation of the form t=some function of v, θ, h.
How far will the sword have traveled horizontally in that time? Get an equation in the form x=some function of v, θ and h.
Knowing x=9m, what equation do you get for θ?

 

[Superman123]

You know the PE stored in the bow. That, we assume, is all turned into KE of the sword. If the sword has mass m and speed v at launch, what is its KE in terms of m and v?

It's KE might be Ek= (m*v^2)/2 and I know that Ek is equal to 179 J, the mass of the sword is also 1.280 kilogrammes. The velocity will be 1.29 m/s

If the throw speed is v and the angle is θ, what are the horizontal and vertical components?

The vertical component is Vy, the horizontal is Vx.

with that vertical velocity, how long will it take to reach its maximum height? Get an equation of the form t=some function of v, θ, h.

As I am trying to figure out the time it takes to reach maximum height, I am only taking the vertical component into consideration. Using the equation V=Vy-at. In his case is the gravitational power and because the speed at maximum height is 0, I rewrote the equation and got t=V sin(θ) / g. From here I got stuck, I couldn't find a way to calculate the time, Many variables are missing and you mentioned h is supposed to be in the function, but I don't have it in t=V sin(θ) / g.

 

[haruspex]

h is supposed to be in the function, but I don't have it in t=V sin(θ) / g.

So you need a SUVAT equation that involves distance, not time. Or, equivalently, you can consider the loss of KE need to reach height h. How much PE does it gain?

 

[Superman123]

Sorry, I just thought about what you said earlier about writing the time as some function of v, θ, h and how long it would take to reach the h with the vertical velocity, Vx. I could write.
tan θ= Vy/Vx.
Vx=Vy/tan θ
I could then write the time as t= h/Vx or t= h/(Vy/tan θ), this function has v, θ and h. Is it right to do this way or am I doing something wrong?

 

[Superman123]

There is another way that you mentioned about a suvat equation that requires distances and that would help me get the time:

s= ut + ½at^2

s = h = ut + ½at^2

= 0t + ½gt^2

making h = ½gt^2

Which makes t= √(2h/g)

I am not sure about this way or the other one, but this way give me an answer to the time.

 

[haruspex]

There is another way that you mentioned about a suvat equation that requires distances and that would help me get the time:

s= ut + ½at^2

s = h = ut + ½at^2

= 0t + ½gt^2

making h = ½gt^2

Which makes t= √(2h/g)

I am not sure about this way or the other one, but this way give me an answer to the time.

Yes, that is the time taken to reach height h. How far does it have to travel horizontally in that time? What does that tell you about the horizontal velocity?

 

[Superman123]

S= 9 meters
s= U* time
s= U√(2h/g)
u=5.85 m/s
Is this correct?

the angle would then be θ=atan(Vy/Vx)
I know Vx, it's 5.58, but how do I determine Vy?

 

[Superman123]

There is another suvat equation that I could use to solve this, but we just used it and I am unsure if it gives the right answer.

Δy=Vy*t+1/2g*t^2

At the top of the height Δy=0

0=Vy(1.537)+1/2(-9.82)(1.537^2)

Vy= 7.5466 m/s

θ=atan(Vy/Vx)
θ=atan(7.54/5.58)

θ=53.52 degrees

 

[haruspex]

s= U√(2h/g)
u=5.85 m/s

You need to bear in mind that in this question we are effectively given the launch speed, and we are now taking the horizontal distance to the wall to be 9m, and the top of the trajectory to be at that distance. This means that the height of the trajectory need not be the height of the wall. We only have to decide whether it will make it over the wall, so it could go higher.
So, yes, s= U√(2h/g), but where h is unknown.

Alternatively, we could suppose it just makes it over the top, calculate the launch speed for that and see whether it exceeds the given launch speed. Either will do, but you need to pick one and stick with it.

 

[Superman123]

OOhh, Well, we can assume that it goes over the wall.

Then U would be
9=U√(2*12/9.82)
U=5.76 m/s; 5.76 < 5.85
What does this tell us, does it just tell us that it requires a lower velocity to get over the wall or that it can't get over the wall from a 9 meters distance?

 

[haruspex]

9=U√(2*12/9.82)
U=5.76 m/s;

I thought the height was 11.6, not 12.
Anyway, let us be clear what you have calculated here. You have effectively said: suppose it just clears the wall; the horizontal velocity needed is 5.76m/s. You now need to figure out whether the total speed required at launch exceeds that available from the bow. I think you previously calculated the vertical speed at launch to reach the top of the wall. How do you combine these two speedcomponents to find the launch speed?

 

[Superman123]

Well, if one speed is 5.85 m/s (did the calculation again with 11.6) and the other one is 7.54 then launch speed is

√(5.58^2+7.54^2)= 9.3 m/s

The speed available from the bow is
179=(1.28 kg *v^2)/2
v=16.703

16.703 > 9.3 , meaning that it doesn't exceed the speed available from the bow and that I can use the given speed.

 

[haruspex]

Well, if one speed is 5.85 m/s (did the calculation again with 11.6) and the other one is 7.54 then launch speed is

√(5.58^2+7.54^2)= 9.3 m/s

The speed available from the bow is
179=(1.28 kg *v^2)/2
v=16.703

16.703 > 9.3 , meaning that it doesn't exceed the speed available from the bow and that I can use the given speed.

Looks right.

 

[Superman123]

Thank you very much, I appreciate your help !
Just a very tiny question, did you use suvat-equations to construct this function for the optimal angle (π-atan(d/h))/2?

 

[haruspex]

Thank you very much, I appreciate your help !
Just a very tiny question, did you use suvat-equations to construct this function for the optimal angle (π-atan(d/h))/2?

Yes.