Chemlach
- 1
- 0
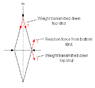
1. The Problem is a simple scissors jack has lifted a 450 kg car and the angle of the arms of the jack are 15° as seen in the attached drawing
2. The question is what is the applied force required to lift the 450 kg mass?
3. I drew my free body diagram and got that F=mg/2cos15°, which comes out to 2280. But the answer is 1180 so I must have missed something. Could you let me know where I went wrong?
2. The question is what is the applied force required to lift the 450 kg mass?
3. I drew my free body diagram and got that F=mg/2cos15°, which comes out to 2280. But the answer is 1180 so I must have missed something. Could you let me know where I went wrong?