- #1
ShizukaSm
- 85
- 0
My physics book when providing proof of the electric potential of a disk tells me that the area of a ring with radius [itex]R'[/itex] and width [itex]dR'[/itex] is [itex]2 \pi R'dR'[/itex]
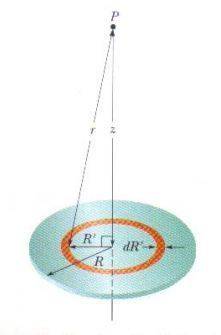
The problem is, I have no idea how he arrives at this conclusion. Here is my attempt:
[itex]A = \pi (R'+dR')^2 - PiR'^2\\ A = \pi(R'^2 + dR'^2 + 2R'dR') - \pi R'^2 \\ A = \pi dR'^2 + 2 \pi R' dR'[/itex]
Which is, of course, different from what my book says:
[itex]A = \pi dR'^2 + 2 \pi R' dR' \neq 2 \pi R'dR' [/itex]
The problem is, I have no idea how he arrives at this conclusion. Here is my attempt:
[itex]A = \pi (R'+dR')^2 - PiR'^2\\ A = \pi(R'^2 + dR'^2 + 2R'dR') - \pi R'^2 \\ A = \pi dR'^2 + 2 \pi R' dR'[/itex]
Which is, of course, different from what my book says:
[itex]A = \pi dR'^2 + 2 \pi R' dR' \neq 2 \pi R'dR' [/itex]