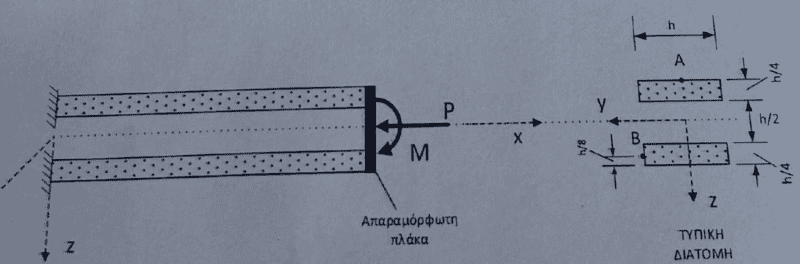
To calculate the stress due to bending moment at point A in a structure with two members connected by a non-deformable plate, you should consider each member individually and determine the neutral axis for each member separately. rsdfgrgvfd
The neutral axis is the axis within a member where the stress due to bending is zero. In a symmetric cross-section, like the one you described, the neutral axis typically passes through the centroid of the cross-section.
For each member (top and bottom), you can assume the neutral axis to be at the centroid of that specific member's cross-section. This means that the neutral axis for the top member is at a distance of h/4 from the top surface, and the neutral axis for the bottom member is at a distance of h/4 from the bottom surface, where 'h' is the height of the entire cross-section.
So, you should analyze each member separately and calculate the bending stress at point A based on the neutral axis position for that member. The stress in the top member and the stress in the bottom member might be different, and you'll need to account for both in your calculations.
In summary, when calculating the stress due to bending at point A, treat each member as an individual beam and determine the neutral axis for each member separately, considering their individual cross-sections and dimensions. :)
