calcphonup
- 4
- 0
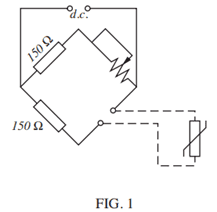
a. The resistance thermometer bridge circuit shown in FIGURE 1 has a designed maximum temperature of 200°C, ignoring the effects of connecting wire resistance. If the connecting loop is 250 m determine the smallest gauge (swg) of copper wire which must be used if the indicated maximum temperature is to be less than 202°C.
The temperature coefficient of resistance of the thermometer is 0.0042 °C–1 and the resistance of the thermometer is 112 Ω at 20°C. Assume the connecting leads are at 20°C.
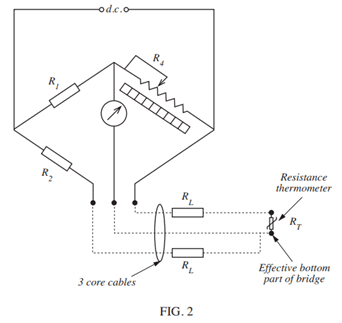
b. Using the gauge of copper wire calculated in part (a), calculate the maximum indicated temperature using a 3-wire system (as shown in FIGURE 2) over a distance of 125 m.Relevant EquationsRt = R0(1 + at)
R1RT = R2RS
R = pL/A = Resistance = (Resistivity) x Length of wire / cross-sectional area
A = (pi x d2) / 4
d = squareroot(4A /pi)
R_t=R_20×(1+α×∆t)
α=0.0042
R20 = 112Ω
∆t=202-20=182
R_t=R_20×(1+α×∆t)
R_t=112×(1+0.0042×182)
R_t= 197.6128
As both resistors on figure 1 are 150Ω, they cancel each other out.
Find the resistivity of copper at 20°C
ρ=RA÷L
Where:
R = Resistance of copper at 20°C
A = area
L = length
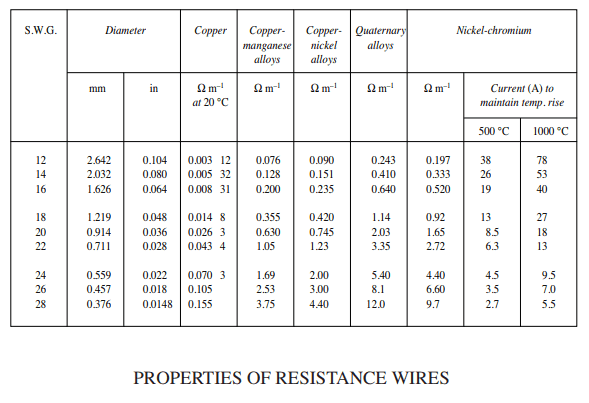
From the properties of resistance wires table:
When diameter = 0.376mm, resistance = 0.155m-1
0.376mm diameter = 0.11103645mm2 for the area.
Converting resistance to per mm = 0.000155m-1
For length 1m = 1000mm.
Therefore, ρ=0.000155×0.111036450÷1000=1.72×10^(-8)
Resistivity of copper wire at 20°C = 1.72×10^(-8)Ωm-1
To find the area the equation would be A=(ρ×L)/R
A=(1.72×10^(-5) Ωmm×250000mm)/197.6128Ω
A = 0.02176mm2
Find diameter = 0.16645mm
Too small of a diameter.
Any help would be greatly appreciated. Ive been stuck for a week
Moderator note: Moved from a technical forum.
The temperature coefficient of resistance of the thermometer is 0.0042 °C–1 and the resistance of the thermometer is 112 Ω at 20°C. Assume the connecting leads are at 20°C.
b. Using the gauge of copper wire calculated in part (a), calculate the maximum indicated temperature using a 3-wire system (as shown in FIGURE 2) over a distance of 125 m.Relevant EquationsRt = R0(1 + at)
R1RT = R2RS
R = pL/A = Resistance = (Resistivity) x Length of wire / cross-sectional area
A = (pi x d2) / 4
d = squareroot(4A /pi)
R_t=R_20×(1+α×∆t)
α=0.0042
R20 = 112Ω
∆t=202-20=182
R_t=R_20×(1+α×∆t)
R_t=112×(1+0.0042×182)
R_t= 197.6128
As both resistors on figure 1 are 150Ω, they cancel each other out.
Find the resistivity of copper at 20°C
ρ=RA÷L
Where:
R = Resistance of copper at 20°C
A = area
L = length
From the properties of resistance wires table:
When diameter = 0.376mm, resistance = 0.155m-1
0.376mm diameter = 0.11103645mm2 for the area.
Converting resistance to per mm = 0.000155m-1
For length 1m = 1000mm.
Therefore, ρ=0.000155×0.111036450÷1000=1.72×10^(-8)
Resistivity of copper wire at 20°C = 1.72×10^(-8)Ωm-1
To find the area the equation would be A=(ρ×L)/R
A=(1.72×10^(-5) Ωmm×250000mm)/197.6128Ω
A = 0.02176mm2
Find diameter = 0.16645mm
Too small of a diameter.
Any help would be greatly appreciated. Ive been stuck for a week
Moderator note: Moved from a technical forum.
Last edited by a moderator:
 ##\qquad ## !
##\qquad ## !