Calculating Critical points for multivariable functions.

[DavidAp]

I am asked to find all local maximum and minimum points for the function,
f(x,y) = (1+xy)(x+y) so, naturally, I had to find the critical points. However, in the back of my book (Calculus Early Transcendentals 6E, James Stewart) the only critical points are (1,-1) (-1,1) (both of which are saddle points but that's not what's important).

My question is, what did I do wrong in my mathematics? I am getting two extra sets of critical points and I'm wondering: did the book forget to mention them as possible points or did I mess up during the calculations? Probably the latter but I checked my math twice, the second time on the board.

I took a picture of my math because it seemed so much easier. Hopefully my hand writing is legible and the picture is big enough.

My critical points are (1,-1) (-1,1) (-2/6, 10/6) (10/6, -2/6)
If the image is illegible please tell me and I will type it all out on text.

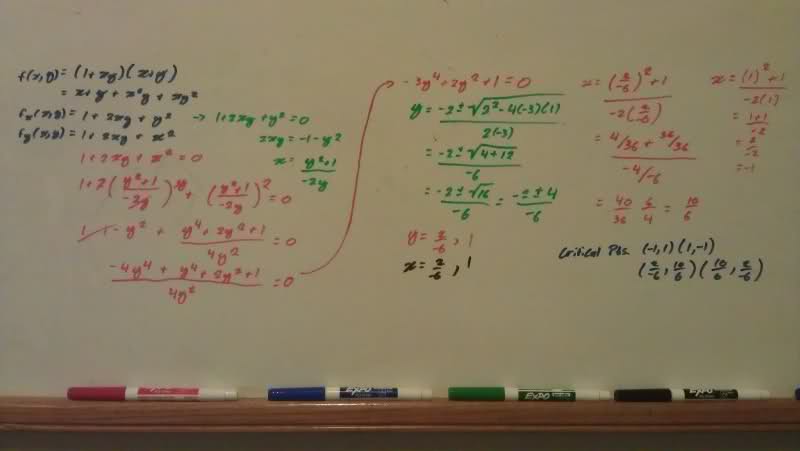
Thank you for reviewing my question, I greatly appreciate it.

 

[Ray Vickson]

f_x = 1+y^2+2xy = 1-x^2 + (x+y)^2, and f_y = 1 - y^2 + (x+y)^2, so if we set s = x+y we have x = +-sqrt(1+s^2) and y = +-sqrt(1+s^2). If we take both + roots (so x,y>0) we have x = y and so s=2x and x = sqrt(1+4x^2), which is impossible. Similarly, we cannot take both - roots, so must take one + and one -. That makes s = 0, and so x = +-1, y = -+1: (1,-1) or (-1,1). Your squarings, etc., have introduced spurious roots (or more precisely, things that are not roots at all). After getting an alleged 'solution' you must always plug it back into the equations (the _original_ ones, not the squared versions) to check if they work.

RGV