Calculating flux through a plane cutting two concentric cylinders

[Zayan]

Homework Statement

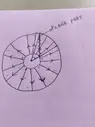
Calculating flux through a plane cutting two concentric cylinders.

Relevant Equations

/integral E.ds = q/e0.

This was asked in an exam. I'll share the photo of the question.

Well firstly as the outer cylinder is grounded, it must have a zero potential. My first doubt is that is it like a capacitor? i.e, will there be any field outside the outer cylinder? If no then how so?

I presumed that it won't have any field lines going out so I only have to calculate the flux through the plane inside the outer cylinder only. Now, since some part of the plane is inside both the cylinders, it must have zero flux as there's no charge enclosed. So I would have to calculate the flux through the two strips which are outside the inner cylinder but inside the outer cylinder. Also the field would be only due to the inner cylinder as the portion is still inside the outer cylinder so no field by the outer one.

Now my second problem is how to calculate the flux. If it were an infinite cylinder I would assume a infinite line charge on the axis of it and simply integrate through the 2 remaining slits slits. But I am unable to do that as I think the stip I'll be choosing would have non uniform field on it so I might have to calculate a double integral which is outside my course.

I've seen some solutions but they do it like it's an infinite cylinder so they just integrate like I mentioned. But I can't seem to figure out if that approach is wrong or not. Also I've seen some solutions calculating the flux with gauss's law, I am doubtful of that too. Can anyone tell me is my reasoning conceptually correct or am I making a conceptual error or maybe missing something.

 

[haruspex]

I would start by figuring out the total flux through the annulus.

 

[Zayan]

I would start by figuring out the total flux through the annulus.

I suppose it would be total charge of the inner cylinder over epsilon-naught.

 

[Gordianus]

I remember Gauss' Law refers to a closed surface. I think the plane isn't a closed one.

 

[Zayan]

Y

I remember Gauss' Law refers to a closed surface. I think the plane isn't a closed one.

Are you referring to my reply or the main question? If it's the reply then yes I know but he asked the "total" flux. So it is q/e⁰.

 

[Steve4Physics]

Well firstly as the outer cylinder is grounded, it must have a zero potential. My first doubt is that is it like a capacitor? i.e, will there be any field outside the outer cylinder? If no then how so?

Maybe you should first understand:
a) what are the charges on the inner and outer faces of each cylinder and
b) what are the electric fields in each region.

Suppose you have the 2 cylinders, initially uncharged.
1) You add charge Q to the inner cylinder; what are the answers for a) and b)?
2) You earth (ground) the outer cylinder; what are the answers for a) and b)?

I suppose it would be total charge of the inner cylinder over epsilon-naught.

Remember the question says that the annular region contains a dielectric.

BTW, if you break large blocks of text into paragraphs, it improves readability.

 

[Zayan]

Maybe you should first understand:
a) what are the charges on the inner and outer faces of each cylinder and
b) what are the electric fields in each region.

Suppose you have the 2 cylinders, initially uncharged.
1) You add charge Q to the inner cylinder; what are the answers for a) and b)?
2) You earth (ground) the outer cylinder; what are the answers for a) and b)?


Remember the question says that the annular region contains a dielectric.

BTW, if you break large blocks of text into paragraphs, it improves readability.

Okay I'll edit it. So for the first question I suppose after charging the inner cylinder, charge get's induced in the outer one too. And after grounding, charge is flown from the outer cylinder to make its potential zero. But I am not quite sure how much. Also, I am not quite sure how to write the potential of a cylinder.

 

[Steve4Physics]

Okay I'll edit it. So for the first question I suppose after charging the inner cylinder, charge get's induced in the outer one too. And after grounding, charge is flown from the outer cylinder to make its potential zero. But I am not quite sure how much. Also, I am not quite sure how to write the potential of a cylinder.

Referring to the Post #6 questions, you didn't actually answer! So, to answer Q1 as an example:

1a) The inner cylinder will have charge Q on its outer surface and zero charge on its inner surface.
The outer cylinder will have charge -Q on its inner surface and charge Q on its outer surface.

1b) The field inside the inner cylinder will be zero.
The field in the annular region (between cylinders) and outside the outer cylinder will be radially symmetric pointing outwards (if Q is positive). The field's magnitude a distance r from the central axis, will be (using Gauss's law) $\frac Q {(2 \pi r l) \kappa \epsilon_0}$ (though this result is not actually needed to answer the Post #1 question).

So your question now is: how does earthing the outer cylinder change the above answers?

Edit: typo's.

 

[Zayan]

Referring to the Post #6 questions, you didn't actually answer! So, to answer Q1 as an example:

1a) The inn.er cylinder will have charge Q on its outer surface and zero charge on its inner surface.
The outer cylinder will have charge -Q on its inner surface and charge Q on its outer surface.

1b) The field inside the inner cylinder will be zero.
The field in the annular region (between cylinders) and outside the outer cylinder will be radially symmetric pointing outwards (if Q is positive). The field's magnitude a distance r from the central axis, will be (using Gauss's law) $\frac Q {(2 \pi r l) \kappa \epsilon_0}$ (though this result is not actually needed to answer the Post #1 question).

So your question now is: how does earthing the outer cylinder change the above answers?

Edit: typo's.

I get the point. Okay let me go through. Firstly the inner one is charged so all charge will be on the outer side of it as the field in the conductor is zero(by gauss's law). And due to that charge a negative charge is induced on the inner side of the outer one(-Q). But since it was neutral, it will have an equal positive charge on the outer side(in accordance with conductors having zero field in thickness). Now we ground the outer cylinder. I get that the potential will be zero of the outer one. But how do you even calculate how much charge will flow to make its potential zero. I can't recall any formula that gives me the potential of a cylinder.

 

[Steve4Physics]

I get the point. Okay let me go through. Firstly the inner one is charged so all charge will be on the outer side of it as the field in the conductor is zero(by gauss's law). And due to that charge a negative charge is induced on the inner side of the outer one(-Q). But since it was neutral, it will have an equal positive charge on the outer side(in accordance with conductors having zero field in thickness)

Yes - almost! Note that if the outer cylinder has an induced charge of -Q on its inner surface, its outer surface must have a charge Q because of charge conservation: the net charge must remain zero. (The zero internal field is not the reason.)

Now we ground the outer cylinder. I get that the potential will be zero of the outer one. But how do you even calculate how much charge will flow to make its potential zero. I can't recall any formula that gives me the potential of a cylinder.

Taking the ground as zero potential is not important - only potential differences actually matter. Taking ground to be at zero potential is just a convenience in some situations. Just like taking infinity as zero potential is sometimes convenient.

'Ground' is treated as an infinite capacitor. It can supply/accept unlimited amounts of charge without changing its potential.

When the outer cylinder is grounded, all the (Q) charge on the outer surface flows to earth. That's because like charges are mutually repulsive - they can flow to earth to get further apart and reduce their potential energy. (Of course, if Q is positive and we are dealing with metallic conductors, it's actually electrons flowing from ground to the cylinder, but the effect is the same as positive charges leaving the outer cylinder.)

The charges on the inner surface of the outer cylinder (-Q) are unaffected- they are 'held' there by attraction from the internal positive charges.

That's a not a very rigorous explanation of course, but might help.

Minor edits.

 

[kuruman]

I can't recall any formula that gives me the potential of a cylinder.

How about using Gauss's Law to calculate the electric field just underneath the surface of the outer cylinder? Set aside the plane the for this calculation and figure out the electric field inside the dielectric. What do you think the closed Gaussian surface should look like?

 

[Zayan]

How about using Gauss's Law to calculate the electric field just underneath the surface of the outer cylinder? Set aside the plane the for this calculation and figure out the electric field inside the dielectric. What do you think the closed Gaussian surface should look like?

I take a cylindrical surface as it is symmetric and calculate the field inside the region with the dielectric and it comes out as Q/2πrle⁰k

 

[Steve4Physics]

I take a cylindrical surface as it is symmetric and calculate the field inside the region with the dielectric and it comes out as Q/2πrle⁰k

According to your attachment, this is before grounding . What effect does grounding have on the answer? (Hint - Post #10.)

In the following diagram the 'ends' of the plane are labelled A and F. Other important points are marked B-E. A horizontal (perpendicular to plane) line has been also been added in case it might be helpful.

Your are going to have to ask yourself what are the individual fluxes through AB, BC, CD, DE and EF. Then add them. If the electric field is zero in any region(s) this will help a lot!

 

[Zayan]

According to your attachment, this is before grounding . What effect does grounding have on the answer? (Hint - Post #10.)

In the following diagram the 'ends' of the plane are labelled A and F. Other important points are marked B-E. A horizontal (perpendicular to plane) line has been also been added in case it might be helpful.
View attachment 361421
Your are going to have to ask yourself what are the individual fluxes through AB, BC, CD, DE and EF. Then add them. If the electric field is zero in any region(s) this will help a lot!

Let me clear this up. What I'm asking is that how do you know that the entire outer charge will be neutralized by grounding, what's the proof for that? Earth makes the potential zero but that doesn't imply the whole charge will be neutralized does it? Also, note that the derivation for the field is for an infinite cylinder, but the question has given the length l. Nevertheless, assuming it is infinite, I can say the flux through C to D will be zero as there is no field inside. The total flux through the plane will only be through the symmetric regions BC and DE.

 

[Steve4Physics]

Let me clear this up. What I'm asking is that how do you know that the entire outer charge will be neutralized by grounding, what's the proof for that? Earth makes the potential zero but that doesn't imply the whole charge will be neutralized does it?

Ground is treated is an 'ideal' charge reservoir. In this case, the complete loss of the outer charges is a consequence of the charges' tendency to attain the state of lowest potential energy due to mutual repulsion (see previous post).

In practice, ground may not be ideal - so some small charge may remain - but the question assumes an ideal (infinite capacitance) ground - that's the conventional understanding of 'ground' in the context of electrostatics.

I can't explain it better. For more info', try a search such as 'why grounding removes charge'.

Also, note that the derivation for the field is for an infinite cylinder, but the question has given the length l. Nevertheless, assuming it is infinite,

The question specifically says "Ignoring edge effects". So the field from the cylinders of length $l$ is identical to the field you would have from a section of length $l$ of an infinitely long cylinder (with the same linear charge density).

I can say the flux through C to D will be zero as there is no field inside. The total flux through the plane will only be through the symmetric regions BC and DE.

Correct - providing the fluxes for sections AB and EF are zero. This is the case if all the
outer charge has flowed to ground (so the field outside the outer cylinder is zero).

So now you are faced with finding the (identical) fluxes through BC and DE.

 

[Zayan]

Ground is treated is an 'ideal' charge reservoir. In this case, the complete loss of the outer charges is a consequence of the charges' tendency to attain the state of lowest potential energy due to mutual repulsion (see previous post).

In practice, ground may not be ideal - so some small charge may remain - but the question assumes an ideal (infinite capacitance) ground - that's the conventional understanding of 'ground' in the context of electrostatics.

I can't explain it better. For more info', try a search such as 'why grounding removes charge'.


The question specifically says "Ignoring edge effects". So the field from the cylinders of length $l$ is identical to the field you would have from a section of length $l$ of an infinitely long cylinder (with the same linear charge density).


Correct - providing the fluxes for sections AB and EF are zero. This is the case if all the
outer charge has flowed to ground (so the field outside the outer cylinder is zero).

So now you are faced with finding the (identical) fluxes through BC and DE.

Okay makes sense. I did not know what edge effects they're referring to. So now my doubt is almost cleared I'll revise the earthing concept. So now for flux I'll calculate it through BC then multiply by two. So I take a strip of l length dx width and find the flux and integrate from π/4 to π/3.

 

[Steve4Physics]

Okay makes sense. I did not know what edge effects they're referring to. So now my doubt is almost cleared I'll revise the earthing concept. So now for flux I'll calculate it through BC then multiply by two. So I take a strip of l length dx width and find the flux and integrate from π/4 to π/3.

Looks like you have correctly found the necessary angles which define each section (BC and DE) of the plane through which flux passes.

Not clear what integral you will take but if done correctly it will lead to the answer.

But there is a (quicker, simpler) way of doing it without integration. If you draw some lines of flux which pass through the (say) BC section near its edges, you might be able to spot it.

 

[Zayan]

Looks like you have correctly found the necessary angles which define each section (BC and DE) of the plane through which flux passes.

Not clear what integral you will take but if done correctly it will lead to the answer.

But there is a (quicker, simpler) way of doing it without integration. If you draw some lines of flux which pass through the (say) BC section near its edges, you might be able to spot it.

Are you talking about the unitary method? Like dividing total flux in 2π and multiplying by 2*15° = 30°? I don't know I am kinda sceptical about that method. Is that valid? I mean the field is not constant for BC so can I still use that?

 

[Steve4Physics]

Are you talking about the unitary method? Like dividing total flux in 2π and multiplying by 2*15° = 30°? I don't know I am kinda sceptical about that method. Is that valid? I mean the field is not constant for BC so can I still use that?

Please post a diagram showing the lines of flux through BC.

 

[haruspex]

Are you talking about the unitary method? Like dividing total flux in 2π and multiplying by 2*15° = 30°? I don't know I am kinda sceptical about that method. Is that valid? I mean the field is not constant for BC so can I still use that?

Picture it first without the plane. You have a total flux through the cylinder, evenly distributed around the circle.
In the 2D diagram, draw a line within the annulus from a point A on the outer cylinder to a point B on it. Doesn’t have to be straight. What fraction of the field lines cross the line an odd number of times?

 

[Zayan]

What fraction of the field lines cross the line an odd number of times?

The same number of lines that would have crossed the part of curved surface of the outer cylinder

Please post a diagram showing the lines of flux through BC.

 

[Steve4Physics]

The same number of lines that would have crossed the part of curved surface of the outer cylinder

OK. In case it's not yet clear, here's a diagram showng field lines (in red) in the region of interest:

The amount of flux through an area can be represented visually by the number of field lines passing through the area.

The lines of flux that pass through BC are the same ones that start on arc CG and end on arc BH because the lines are radial. (*See note at end.)

So the flux through BC equals the flux from arc CG. In my diagram this is equivalent to the 3 red lines.

If the total flux from the inner cylinder is $\Phi$ then the fraction of this flux which starts on arc CG (and passes through BC) is, by proportion, $\frac {15}{360} \Phi$. This is the flux through BC.

*Note: The area in question is actually a rectangular region of the plane with length $l$ and width BC. But is is more convenient to refer to this area simply as ‘BC’. Similarly elsewhere.

Minor edit.

 

[Zayan]

OK. In case it's not yet clear, here's a diagram showng field lines (in red) in the region of interest:
View attachment 361435
The amount of flux through an area can be represented visually by the number of field lines passing through the area.

The lines of flux that pass through BC are the same ones that start on arc CG (and end on arc BH) because the lines are radial. (*See note at end.)

So the flux through BC equals the flux from arc CG. In my diagram this is equivalent to the 3 red lines.

If the total flux from the inner cylinder is $\Phi$ then the fraction of this flux which starts on arc CG (and passes through BC) is, by proportion, $\frac {15}{360} \Phi$. This is the flux through BC.

*Note: The area in question is actually a rectangular region of the plane with length $l$ and width BC. But is is more convenient to refer to this area simply as ‘BC’. Similarly elsewhere.

Yes I understand that I even said it. My point is that even though the field on the plane area is not uniform, we can equate it with the flux passing through the cylindrical arc without doing the calculation? I suppose that even though the field is higher on the actual plane but the angle and the area difference between the plane and the curved surface equalize themselves to give the same flux. I think that is what's happening

 

[Steve4Physics]

Yes I understand that I even said it. My point is that even though the field on the plane area is not uniform, we can equate it with the flux passing through the cylindrical arc without doing the calculation?

You can't equate the field on a plane and flux through the plane. They are different quantities. You can calculate the flux from the field: $\phi = \int_A \vec E \cdot \vec {dA}$.

Doing the integral is equivalent to counting the lines passing through the area.

In this problem there is no need to do the integral. You can directly count the lines, as explained in Post #22.

I suppose that even though the field is higher on the actual plane but the angle and the area difference between the plane and the curved surface equalize themselves to give the same flux. I think that is what's happening

Yes. You will get the same answer whichever method you use. But make sure you understand why the quicker method works - it can make some problems much easier.

 

[Zayan]

You can't equate the field on a plane and flux through the plane. They are different quantities. You can calculate the flux from the field: $\phi = \int_A \vec E \cdot \vec {dA}$.

Doing the integral is equivalent to counting the lines passing through the area.

In this problem there is no need to do the integral. You can directly count the lines, as explained in Post #22.


Yes. You will get the same answer whichever method you use. But make sure you understand why the quicker method works - it can make some problems much easier.

Yes I meant to say that even though the fields are not uniform, we can equate the "flux" of that region as the decrease in flux and the increase of cos/theta sort of cancel each other out

 

[Steve4Physics]

Yes I meant to say that even though the fields are not uniform, we can equate the "flux" of that region as the decrease in flux and the increase of cos/theta sort of cancel each other out

Yes. I assume that theta means the angle between an area-element and the field.

As well as theta, the distance from the axis affects field strength; this must also be accounted if using integration.

 

[Zayan]

Yes. I assume that theta means the angle between an area-element and the field.

As well as theta, the distance from the axis affects field strength; this must also be accounted if using integration.

check this out