Calculating Forces and Acceleration Between Charged Particles

[thst1003]

An electron is near a positive ion of charge +9e and a negative ion of charge −8e (see the figure below). (Take a = 5.23 µm, b = 4.28 µm, and θ = 54.9°.)

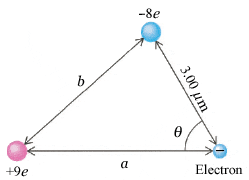
(a) Find the magnitude and direction of the resultant force on the electron. (Let right be the +x-direction. Measure the angle counter-clockwise from the +x-axis.)

(b) Find the magnitude and direction of the electron's instantaneous acceleration (Let right be the +x-direction. Measure the angle counter-clockwise from the +x-axis.)

I used the equation F=kqq'/r² and I got the forces that came in and out of the single electron (Remember e=1.6e-19 C). I got those values to be 3.96e-19 N from the bottom left charge to the single electron and 6.137e-18 N from the top charge to the single electron. I am having difficulty making sure those are correct and solving for the actual answers. I don't even know how to do part b. I am assuming it deals with the force calculated and the mass of the electron.

 

[cepheid]

The force due to the bottom left charge points in the -x-direction. The force due to the top charge points at an angle of 54.9 degrees from the -x axis (which means it points at an angle of 180 minus that as measured from the +x axis). You have to find the vector sum of these two forces. One easy way of doing this is to resolve each of them into x and y-components, add up these components separately, and then compute the magnitude of the result.

I don't get the same answers as you for the magnitudes of the forces. Can you post your calculations?

EDIT: No, sorry, I messed up on that slightly. The second force points at an angle of 54.9 degrees *below* the +x-axis. I.e. you start from the +x-axis and rotate clockwise by 54.9 degrees. So, using the convention they asked you to use, this angle is interpreted as -54.9 degrees.