Calculating Frictional Force: L, Lh, Lv, m

  • Context: Undergrad 
  • Thread starter Thread starter adjacent
  • Start date Start date
  • Tags Tags
    Force Frictional force
Click For Summary
SUMMARY

The discussion focuses on calculating the frictional force acting on a ladder, specifically in terms of its length (L), horizontal distance (Lh), vertical distance (Lv), and mass (m). The participants emphasize that when the ladder is stationary, the sum of the horizontal forces, vertical forces, and torques must equal zero. By establishing and solving these equations, one can determine the force F and the coefficient of friction necessary to prevent the ladder from slipping. Additionally, the forces acting on the wall are also considered in the calculations.

PREREQUISITES
  • Understanding of static equilibrium in physics
  • Knowledge of torque and its calculation
  • Familiarity with frictional force concepts
  • Basic algebra for solving equations
NEXT STEPS
  • Study the principles of static equilibrium in detail
  • Learn how to calculate torque in various scenarios
  • Explore the coefficient of friction and its applications
  • Investigate real-world examples of frictional forces in engineering
USEFUL FOR

Physics students, engineering students, and professionals involved in mechanics or structural analysis will benefit from this discussion, particularly those interested in understanding frictional forces and static equilibrium in practical applications.

adjacent
Gold Member
Messages
1,552
Reaction score
62
attachment.php?attachmentid=64866&stc=1&d=1387267221.png


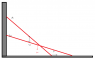
Look at line a,assume it is not sliding down.Line b is sliding down,which means the frictional force of floor is smaller than F.
Line is of mass 1kg.Length is 2m, so C.M is in 1m
How do you find the force F interms of L,Lh, Lv,m each case?
L is the length of line. Lh is the horizontal distance. Lv is Vertical distance.
This is not a Home work Question or Homework type question .
I am just curious.
 

Attachments

  • Untitled.png
    Untitled.png
    2.4 KB · Views: 524
Physics news on Phys.org
You also need to consider the force on the wall.

If the ladder isn't moving (yet) then three things sum to zero..

The horizontal components of the forces
The vertical components of the forces
The torques.

By writing and solving these equations you can solve for the force F or work out the coefficient of friction required to stop the ladder slipping etc
 
  • Like
Likes   Reactions: 1 person
CWatters said:
You also need to consider the force on the wall.

If the ladder isn't moving (yet) then three things sum to zero..

The horizontal components of the forces
The vertical components of the forces
The torques.

By writing and solving these equations you can solve for the force F or work out the coefficient of friction required to stop the ladder slipping etc
Great Idea.Thanks.
 

Similar threads

Undergrad Determine if the block will slide or flip over after contact
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Rolling Without Slipping
  • · Replies 59 ·
2
Replies
59
Views
5K
Undergrad Solving Wheel Coming to a Stop: FBD, Friction & Hysteresis
  • · Replies 22 ·
Replies
22
Views
5K
Undergrad [Question] Calculating the force generated by a tarp hung between two walls
  • · Replies 14 ·
Replies
14
Views
2K
Undergrad Origin of Centripetal force when the net force toward the center is 0?
  • · Replies 8 ·
Replies
8
Views
3K
High School Normal Force Discrepancy for Wedge Vs. Ramp
  • · Replies 9 ·
Replies
9
Views
4K
Undergrad Dumbbell Sliding on Wall: Find Speed of Weights at Equal Velocity
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad Distance traveled by a ball down a ramp and on a flat path
  • · Replies 12 ·
Replies
12
Views
4K
Undergrad Equation of motion for a simple mechanical system
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad How to Calculate force exerted on a falling body?
  • · Replies 12 ·
Replies
12
Views
3K