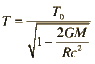aaron35510
- 6
- 0
First of all, (following Einstein's theory of Gravitational Time Dilation (I'll just call it GTD,)) objects (such as us) age slower near strong gravitational fields than in empty space. The higher the local distortion of spacetime due to gravity, the more slowly time passes. So according to GTD, we should pretty much not age at all if were able to survive in a black hole.
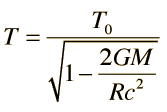 is the formula for GTD, so in that case, a black hole has INFINITE mass (m=infinity), which means that the formula is (original time outside/ infinity.) Therefore, if let's say the time OUTSIDE of the black hole was 50 years, then the time you spent INSIDE the black hole (dilated time) was an infinite amount of time? That doesn't make sense.
is the formula for GTD, so in that case, a black hole has INFINITE mass (m=infinity), which means that the formula is (original time outside/ infinity.) Therefore, if let's say the time OUTSIDE of the black hole was 50 years, then the time you spent INSIDE the black hole (dilated time) was an infinite amount of time? That doesn't make sense.