Philip Wood said:
CAB: I agree with the general thrust of your answer, but don't like your use of X_L = \omega L, because this is only applicable when a sinusoidal current is flowing. In the case of an arbitrary movement of the rod on the rails we have to use the more general term E_{back} = - \frac{d\widetilde{\Phi}}{dt} in which \widetilde{\Phi} is the flux due to the induced current, if any. This emf acts in the opposite direction to BLv (in which B is the externally applied field), and doesn't act at all if the circuit is open.
[Original post corrected.]
But any waveform can be resolved into a sum of sine and cosine functions. Even a non-periodic waveform has a Fourier transform. This seems to annoy everybody. Induction motors are a prime example of induction taking place in a loop with very low R value.
If induced emf was constant independent of load such as self inductance, then the power would increase w/o limit as R decreases. We already know that as the rotor R value decreases, power in heating said rotor increases until R equals X
L. Then as R drops below X
L, rotor heat goes DOWN. This is due to self inductance.
Thus for ac domain, I = Voc/(√R
2 + X
L2). For R << X
L, I = Voc/R.
In your example, if open circuit voltage is "Blv", with the loop resistance of R and inductance L, we cannot ignore L unless we know it is << RT, where T is pulse width. We discussed a transient case in another thread where I included time constants. If L is small, and the induced voltage waveform is a rectangular pulse, that is L/R time constant << T (pulse width), we can assume I = Voc/R. But if L/R approaches or exceeds T, then, I = (Voc/R)(1 - e
-Rt/L).
Here L is increasing as loop area increases. If the track was infinite in length, we would need to compute the Voc waveform. A ramp would result for a dc flux value. The ramp is a constant times "t" (time). The slope of this ramp must be compared to R/L. If slope << R/L, then L will influence the value of I. Later tonight after work, I can compute the infinite track case, slope, then compute L/R constant and its influence.
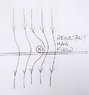
In technician's sketches, please refer to the current in the rod and associated magnetic field. The rod current is part of the loop which includes the track and closed end as well. Using right hand rule, the flux due to current is oriented exactly opposite to external flux. I will draw a sketch for that as well.
Motor/generator textbooks laid this issue to rest in 19th century. The current I is not simply Voc/R. It could be for small L value, but in general L cannot be ignored in loops with very low R. In this example the track and rod are metal such that R is very low. L comes into play in these scenarios. More later.
Claude