Calculating Maximum Pressure for T6 Aluminium Cylinder

[perky416]

Hi guys,

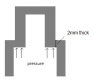
The imagine the picture attached is a cross section of a cylinder. How would I work out the maximum amount of pressure this can be exposed to before the metal shears off at the location labelled "2mm thick"?

Lets say the following material is used:

T6 Aluminium
Ultimate Tensile Strength - 310 MPa
Tensile Yield Strength - 276 MPa
Shear Strength - 207 MPa

Iv googled and googled but can only seem to find information relating to shear force in beams or punching through a material.

All help greatly appreciated.
Thanks

 

[Nidum]

Imagine the small diameter section being separate and fitting into the larger diameter part like a piston in a cylinder . The contact area between the two parts represents the area carrying the shear force in the one piece object

 

[perky416]

Hi,

I understand the location, its pretty much where iv marked with a black line on the diagram, I just can't for the life of my figure out how to calculate the max force.

Regards

 

[Nidum]

You may be confused by the blind bore . Pressure acts where you have shown it but also on the area at top of the blind bore . Effectively you can ignore the details of the bore and just treat the upper component as if it was solid for purposes of calculating the effective 'piston area' that pressure acts on .

 

[perky416]

Hi,

Sorry reading my post back I understand I wasn't clear, I don't mean where the arrows are I mean where I've done the black line and labeled it 2mm thick i.e. "the contact area between the 2 parts".

 

[Nidum]

It's getting late now . Hopefully someone else will pick up this thread but if not I'll get back to you tomorrow .

 

[perky416]

ok thank you

 

[boneh3ad]

You know how to calculate the upward force due to pressure on that upward piece correct? Don't forget to include both the very top and the two horizontal surfaces toward which you have the arrows pointing in your picture.

 

[perky416]

Sorry not too sure what you mean. Please could you elaborate a little?

 

[boneh3ad]

Well if you want to know the shear stress where those black lines are, you need two things: a force and an area. So, do you know how to calculate the force you need? What about the area?

 

[perky416]

Oh i see what you mean.

The total area that the pressure is acting on including the upward area is 3.14cm^2.

For the force cam i simply convert the pressure? For example 100 bar of pressure = 101.972 kgmf/cm^2.

 

[boneh3ad]

The total area that the pressure is acting on including the upward area is 3.14cm^2.

So the inner diameter of your larger part of the cylinder is 2 cm?

For the force cam i simply convert the pressure? For example 100 bar of pressure = 101.972 kgmf/cm^2.

You are probably better off doing everything in the MKS units (meter, kilogram, second), so that you do pressure in pascals, force in Newtons, and area in m². What you suggest would work but keeping units straight will be more of a pain.

 

[perky416]

Yes 2cm diameter is correct.

So using MSK...
Pressure = 100,000 Pa
Force = 100,000 N/m^2
Area = 0.0314 m^2

Where do I go from here?

 

[boneh3ad]

Yes 2cm diameter is correct.

So using MSK...
Pressure = 100,000 Pa
Force = 100,000 N/m^2
Area = 0.0314 m^2

Where do I go from here?

Well first, force is not measured in N/m². Both of your first two numbers are pressures since Pa = N/m².

Second, you have to add a couple extra zeros to your area because 1 cm x 1 cm is not 0.01 m; it is 0.0001 m.

Then, how do you feel you should proceed to find the force? What does pressure actually mean and how does it relate to force?

 

[perky416]

Ahh we are getting there...

Pressure is force applied to the surface so to speak.

Pressure = force / area.

Which gives us...

Force = pressure x area.
Force = 100,000Pa x 0.000314m^2
Force = 31.4N

 

[boneh3ad]

Alright, so now you have a force. Now you have to convert that back into a stress in the region your are interested. Stress is also a force per unit area, but unlike pressure, it can occur in solids and can occur in shear rather than just normal to a surface. Essentially, pressure is the normal component of stress in a fluid.

Anyway, so you need to find the shear stress. You have a force. You need an area.

 

[perky416]

When you say area do you mean the area where the stress will occur?

If so would it be the circumference x thickness?
62.83mm x 2mm =125.66mm^2 or 0.00012566m^2

Or am i completely off the mark?

 

[boneh3ad]

No you're still heading in the right direction (though I didn't check your math).

 

[perky416]

Ok so if we used Shear stress = force/ area

Shear stress = 31.4N / 0.00012566m^2
Shear stress = =249,880.63 Pa

Should i factor in the strength of the material? For example wouldn't steel be able to handle more pressure than aluminium?

(Ps i really really appreciate all your help, thank you)

 

[boneh3ad]

The strength of a material plays into the maximum stress before failure but does not affect the stress in the shape for a given set of forces.

 

[perky416]

Hi,

Sorry perhaps I didnt make it clear enough in my first post. Thats what I was trying to calculate the max amount of pressure before failure, before the material shears off at the point labelled "2mm thick".

 

[boneh3ad]

Well then you just have to work backward. You know the shear strength of your material already, so work through the problem the opposite direction to calculate the maximum pressure.

 

[Nidum]

I see that this question has appeared on EngineersEdge . You say there that your working pressure will be 250 bar .

To ensure that even a small pressure vessel is safe for that pressure requires a more comprehensive strength analysis than we have talked about so far .

If you want to discuss this topic further please explain what you are actually trying to do .

 

[perky416]

I am making modifications to my air rifle, this part in question is the fill valve. Since posting on engineers edge I machined the part with the labeled 2mm dimension to 4mm as that was the dimension on the original part. After testing it I was happy that it was safe to use and it has worked fine ever since.

I am trying to increase air capacity by freeing up as much space as possible. I wanted to calculate the maximum pressure that a 2mm thickness could take before yield.

I have stirred up a hornets nest previously when working with pressure so I think its worth mentioning the safety precautions taken:
1st I make sure I am satisfied with the calculations, if they check out then I move onto machining and testing. Although previously I only calculated the pipe bursting pressure I used the same corss section dimensions on the original part and I am using a material with a higher yield and tensile strength.
To test previously I placed it in a hole 1ft deep, packed it over with soil...placed a concrete slab on top and filled to around 300 bar, let it settle & vent 10 times, compared post test dimensions to pre test dimensions and inspected it under a microscope for signs of stress.
Next time around testing will be done to 385 bar and be done with water to reduce risks in case of failure.

Regards