Engineering Calculating Power Losses in an AC Induction Motor

[Martin Harris]

Homework Statement

Induction Motor calculation

Relevant Equations

$$Psn (stator nominal power) = Pelectrical (electrical input power)$$
$$Psn (stator nominal power) = \frac {Pn} {efficiency}$$
$$sn(nominal slip) = \frac {Ljr} {Pelectromagnetic} $$
$$ Ωn (nominal speed) = Ωs * (1-sn)$$
$$Mn(nominal torque) = \frac {Pn} {Ωn}$$
$$ILs (stator line current) = \frac {Psn} {sqrt(3) * uls * cosφ}$$

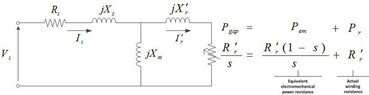
Given the AC Induction (asynchronous motor) in 3 phases:

Parameter	Value
Pn (Nominal Power) = Pmechanical (output power at the shaft)	5 kW = 5000W
uls (Voltage through the stator line)	220 V
fstator (stator frequency)	50 Hz
p (Number of pole pairs)	2
LFe (Iron loss) = Lmechanical (mechanical loss)	LFe = Lmechanical 1.5% Pn
Lv (Ventilation loss on the rotor)	Lv = 1%*Pn
LJr (Rotor Joule loss) = (2/3) * LJs (Stator Joule loss)	#To be calculated below#
η (efficiency of the induction motor)	0.9
cosφ (power factor)	0.88

Requirements:
a) Power loss calculation, Power loss balance.
b) sn (nominal slip) = ? Ωn (Nominal speed) = ? Mn (nominal torque) = ?
c) ILs (current through the statoric line) = ?

Attempt at a solution:
a) LFe= Lmechanical = $$ \frac {1.5} {100} * 5000 W = 75 W$$
Hence, LFe = Lmechanical = 75W (Iron loss = Mechanical loss = 75W)

Lv = $$ \frac {1} {100} * 5000 W = 50 W$$
Hence Lv = 50W (ventilation loss on the rotor)Psn (stator nominal power) = Pelectrical (electrical input power) = $$\frac {Pn} {0.9} = 5555.5555555555555555555555555556 W$$

i) $$ Ljs + Ljr = Psn - (Pn+Lfe + Lmechanical +Lv) = 5555.555555555555556 W - 5200W$$
$$ Ljs + Ljr = 355.5555555555555555555555555556W $$

ii) $$Ljr = \frac {2} {3} * Ljs$$

from i) and ii)
$$Ljs = 213.33333333333333333333333333336 W $$
$$Ljr = 142.22222222222222222222222222224 W $$

$$ Pelectromagnetic (electromagnetic power) = Psn(input electrical power) - Ljs - LFe $$
$$ Pelectromagnetic= 5555.55555555555555556 W - 213.33333333333333333333336 W - 75W $$
$$ Pelectromagnetic = 5267.2222222222222222222222222222 W$$

$$Ltotal (totalloss) = Ljs+LFe+Ljr+Lmechanical+Lv = 555.5555555555555555556 W$$
$$Ltotal (totalloss) = 555.5555555555555555555555555556 W$$
b) $$sn(nominal slip) = \frac {Ljr} {Pelectromagnetic}$$
$$sn= \frac {142.22222222222222222222222222224 W} {5267.2222222222222222222222222222 W } $$
$$sn(nominal slip) = 0.02700137116337939035966670182471 [-] $$

$$ Ωn (nominal speed) = Ωs * (1-sn)$$

where Ωs is the (synchronization speed)

$$Ωs = \frac {2*π*fstator} {p} = \frac {2*π*50Hz} {2} =157.07963267948966192313216916398 [rad/s] $$
$$Ωn (nominal speed) = 157.079632679489661923132 [rad/s] * (1-0.027001371163379390359)$$
$$Ωn = 152.838267215303462845785704096[rad/s]$$

$$ns (syncrhonization speed) [rpm] = \frac {60*fstator} {2} = 1500 [rpm]$$
$$nn (nominal speed) [rpm] = ns*(1-sn) = 1500 [rpm] * (1-0.02700137116337939035966670)$$
$$nn (nominal speed) [rpm] = 1459.4979432549309144604999472629 [rpm] $$

$$Mn(nominal torque) = \frac {Pn} {Ωn} = \frac {5000W} {152.83826721530346284578570409637 [rad/s]}$$
$$Mn(nominal torque) = 32.714320118249532323572617030565 [Nm] $$

c) $$Psn (electrical power input) = sqrt(3) * uls * ILs * cosφ$$
Hence
The current through the stator line:

$$ILs = \frac {Psn} {sqrt(3) * uls * cosφ} = \frac {5555.5555555555555555555555555556 W} {sqrt(3) * 220V * 0.88}$$
$$ILs = 16.567673013935541910845637640667 [A]$$

I would be more than grateful if someone can confirm these calculations.
Many thanks!

 

[Babadag]

Your calculation, it seems to me, is o.k. I have only the following remark:
If according to Steinmetz schematic diagram of an induction motor Rr*(1-sn)/sn*Ir^2=Pn then Rr*Ir^2=Ljr=sn*(Pn+Ljr) and sn=Ljr/(Pn+Ljr)
Now if Pinput-Ljs=Pn+Ljr then sn is o.k. However, Pinput=Pn/0.9=5555.56 and Ljs=213.33 then Pinput-Ljs=5342.2 and Pn+Ljr=5000+142.2=5142.2 W .In this case sn=0.02766.

 

[Babadag]

Usually, in IEC World, 220 V it is the line-to-neutral voltage and the line-to-line is 380 V [now according to IEC std 60038 has to be 400/231 V]

 

[Dr.D]

It is pretty hard to justify so many decimal places when the input values are not nearly so precisely given.

 

[Martin Harris]

Your calculation, it seems to me, is o.k. I have only the following remark:
If according to Steinmetz schematic diagram of an induction motor Rr*(1-sn)/sn*Ir^2=Pn then Rr*Ir^2=Ljr=sn*(Pn+Ljr) and sn=Ljr/(Pn+Ljr)
Now if Pinput-Ljs=Pn+Ljr then sn is o.k. However, Pinput=Pn/0.9=5555.56 and Ljs=213.33 then Pinput-Ljs=5342.2 and Pn+Ljr=5000+142.2=5142.2 W .In this case sn=0.02766.

Thanks for the reply it's much appreciated.
I was told $$\frac {Ljr} {Ljs} = \frac {2} {3}$$
I was just given the following formula:
$$sn = \frac {Ljr} {Pelectromagnetic} $$
where sn = nominal slip, Ljr = 142.2222 W and Pelectromagnetic = Psn - Ljs - LFe = 5555.5555W - 213.3333W - 75W = 5267.2217 W

Hence I get sn (nominal slip) = 0.02700
I don't get where I am comitting the mistake.

 

[Martin Harris]

Usually, in IEC World, 220 V it is the line-to-neutral voltage and the line-to-line is 380 V [now according to IEC std 60038 has to be 400/231 V]

Yes, indeed, I was told that, but asked to use the stator line voltage at 220V and frequency at 50 Hz, but I get what you mean, that's right.

 

[Martin Harris]

It is pretty hard to justify so many decimal places when the input values are not nearly so precisely given.

Indeed, though the result won't change by a lot, even if I trim down the decimals.

 

[Babadag]

By-the -way, in my opinion the power losses Lfe and Ljs may be extracted from rated stator power and ventilation and friction [mechanical losses] from Pgap [then Pgap=Lv+Lmech+Pn+Ljr] neglecting Lfe for rotor where the frequence is very low [sn*fstator] and the iron losses depend on B[magnetic flux density] and frotor.