Calculating Power Lost in a Resistor (within Transformer Circuit)

[Master1022]

Homework Statement

Calculate the power lost via copper loss and iron loss?

Relevant Equations

$P = IV = I^2 R$

Hi,

I have a simple question that I don't have a fundamental understanding of: do resistors dissipate reactive power (in addition to active power)?

For context, when we are looking at a transformer (single phase) equivalent circuit (similar to the one in the image attached), we are asked to find the copper loss (power dissipated in $R_2 = 0.05 \Omega$) and the iron loss (power dissipated in $R_0$ in the primary). From earlier parts of my homework question, we find the phasor diagrams to be: (in the attached images)

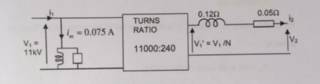
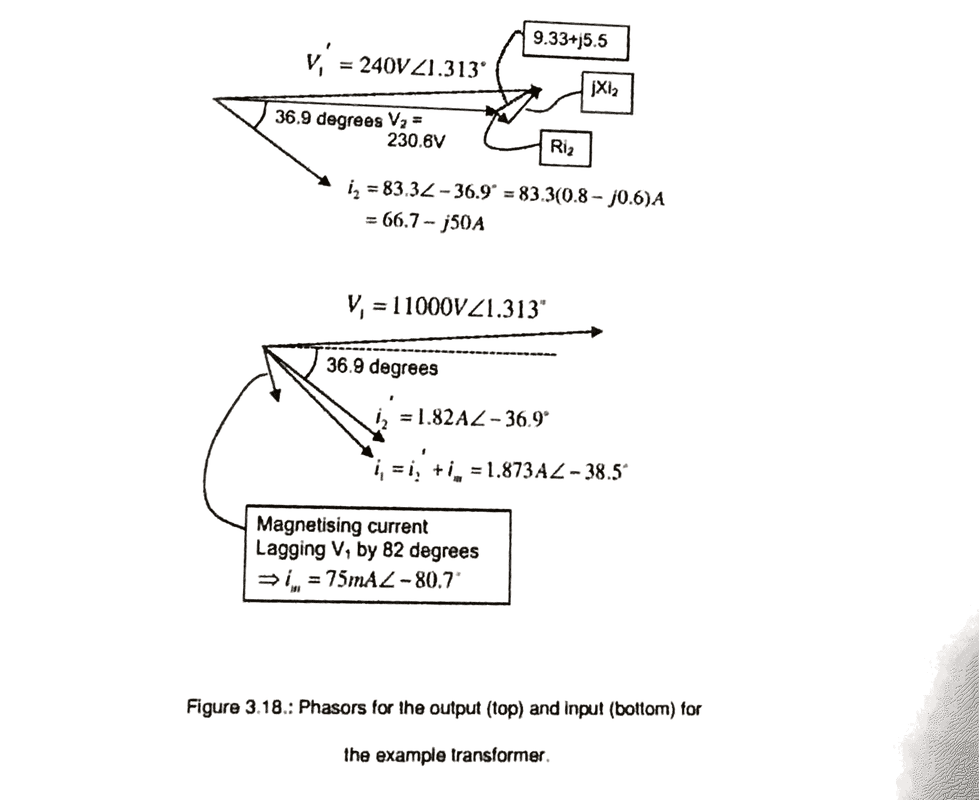
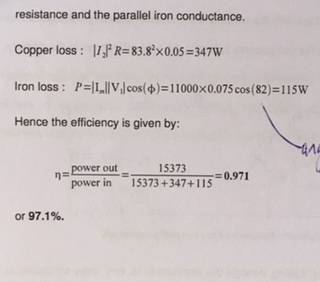
We know that the secondary current $I_2$ is lagging behind $V_2$. $P_{R_2} = |I_2|^2 R_2$ is used even though there is a phase difference. Why is this the case - doesn't this include reactive power as well as active power?

Also, when finding the iron loss, we use the formula $P_{R_0} = |I_m||V_1| cos(\phi)$, where $\phi$ is the power factor.

I can't seem to understand why these formulae are accounting for complex parts of the power as well (or maybe I am misunderstanding them?).

Any help is greatly appreciated.

 

[BvU]

We know that the secondary current $I_2$ is lagging behind V_2. $P_{R_2}=|I_2|^2R_2$ is used even though there is a phase difference. Why is this the case - doesn't this include reactive power as well as active power?

$I_2$ is not lagging behind the voltage over $R_2$, which -- of course -- is $I_2R_2$

 

[Master1022]

$I_2$ is not lagging behind the voltage over $R_2$, which -- of course -- is $I_2R_2$

Thank you very much for your fast reply. Yes, that makes sense to me. How about the core loss? The diagram on the web-page has slightly different labeling (as you have probably picked up), such that $I_m$ is defined to be the sum of the currents going into the parallel components. Doesn't $IVcos(\phi)$ project $I_m$ (as defined in my image) onto $V_1$, which has imaginary components? Why isn't there another projection onto the real axis (i.e. using a cos(1.313 degrees)) ?

 

[BvU]

Confused -- don't remember your circuit diagram being there when I replied.

$V_1$, which has imaginary components

Seems it does. What's the full problem statement ?

 

[Master1022]

Confused -- don't remember your circuit diagram being there when I replied.

Seems it does. What's the full problem statement ?

Sorry, it wasn't - I edited the post recently to include it in order to avoid future confusion when referring to variable names. The original problem overall was:
"A single phase 11kV to 240V transformer is "rated" as 20 kVA. Its magnetising current is 75 mA lagging the supply voltage by 82 degrees. X is 0.12 $\Omega$ and R is 0.05 $\Omega$, both referenced to the secondary. " This final part is about calculating the efficiency and we need the aforementioned power losses.

However, upon second thought, it seems wrong for me to suggest the complex nature of the voltage $V_1$ as all the phasors are drawn relative to $V_2$, which was probably chosen as there was an intermediate question voltages at the secondary terminals (and comparing it to our theoretical expectation of 240 V). Therefore, that arbitrary choice of phasor drawing shouldn't change the physics of the power dissipated, it should always be IVcos($\phi$) between the respective current and voltage. I am not sure if I have conveyed that thought in the most comprehensible manner, please let me know if that doesn't make sense (or if it is incorrect).