- #1
Master1022
- 611
- 117
- Homework Statement
- Calculate the power lost via copper loss and iron loss?
- Relevant Equations
- [itex]P = IV = I^2 R [/itex]
Hi,
I have a simple question that I don't have a fundamental understanding of: do resistors dissipate reactive power (in addition to active power)?
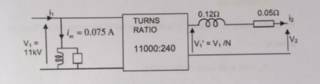
For context, when we are looking at a transformer (single phase) equivalent circuit (similar to the one in the image attached), we are asked to find the copper loss (power dissipated in [itex] R_2 = 0.05 \Omega [/itex]) and the iron loss (power dissipated in [itex] R_0 [/itex] in the primary). From earlier parts of my homework question, we find the phasor diagrams to be: (in the attached images)
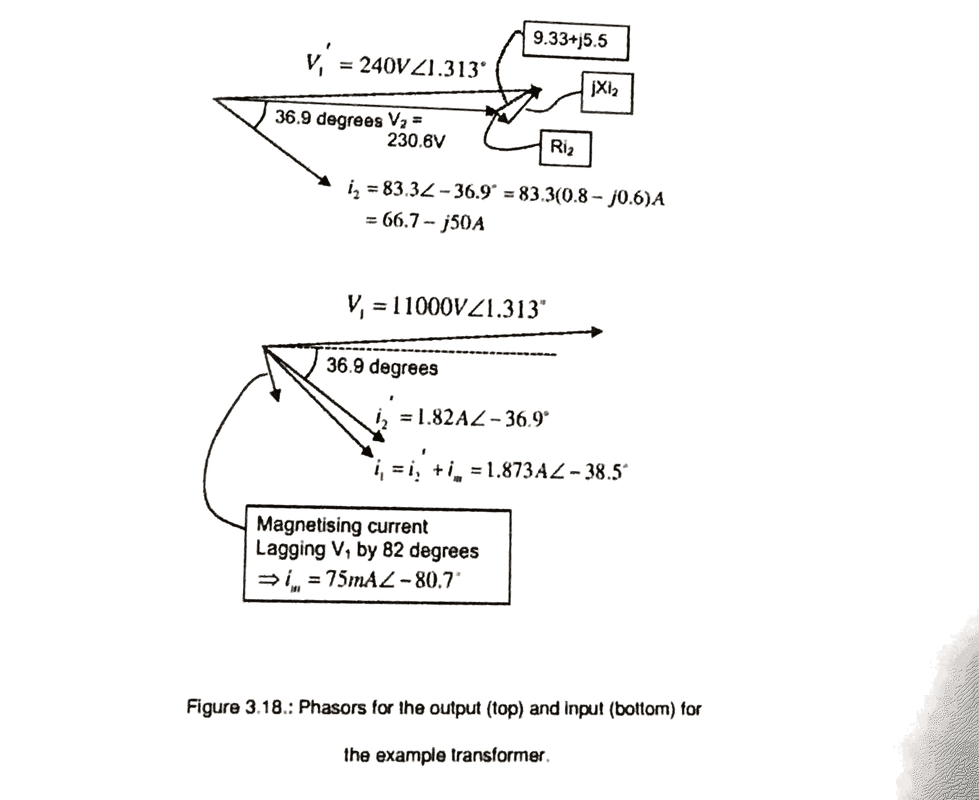
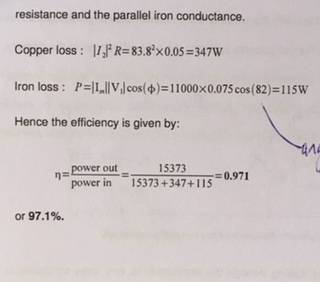
We know that the secondary current [itex] I_2 [/itex] is lagging behind [itex] V_2 [/itex]. [itex] P_{R_2} = |I_2|^2 R_2 [/itex] is used even though there is a phase difference. Why is this the case - doesn't this include reactive power as well as active power?
Also, when finding the iron loss, we use the formula [itex] P_{R_0} = |I_m||V_1| cos(\phi) [/itex], where [itex] \phi [/itex] is the power factor.
I can't seem to understand why these formulae are accounting for complex parts of the power as well (or maybe I am misunderstanding them?).
Any help is greatly appreciated.
I have a simple question that I don't have a fundamental understanding of: do resistors dissipate reactive power (in addition to active power)?
For context, when we are looking at a transformer (single phase) equivalent circuit (similar to the one in the image attached), we are asked to find the copper loss (power dissipated in [itex] R_2 = 0.05 \Omega [/itex]) and the iron loss (power dissipated in [itex] R_0 [/itex] in the primary). From earlier parts of my homework question, we find the phasor diagrams to be: (in the attached images)
We know that the secondary current [itex] I_2 [/itex] is lagging behind [itex] V_2 [/itex]. [itex] P_{R_2} = |I_2|^2 R_2 [/itex] is used even though there is a phase difference. Why is this the case - doesn't this include reactive power as well as active power?
Also, when finding the iron loss, we use the formula [itex] P_{R_0} = |I_m||V_1| cos(\phi) [/itex], where [itex] \phi [/itex] is the power factor.
I can't seem to understand why these formulae are accounting for complex parts of the power as well (or maybe I am misunderstanding them?).
Any help is greatly appreciated.
Last edited:
 Confused -- don't remember your circuit diagram being there when I replied.
Confused -- don't remember your circuit diagram being there when I replied.