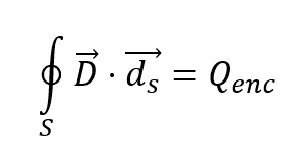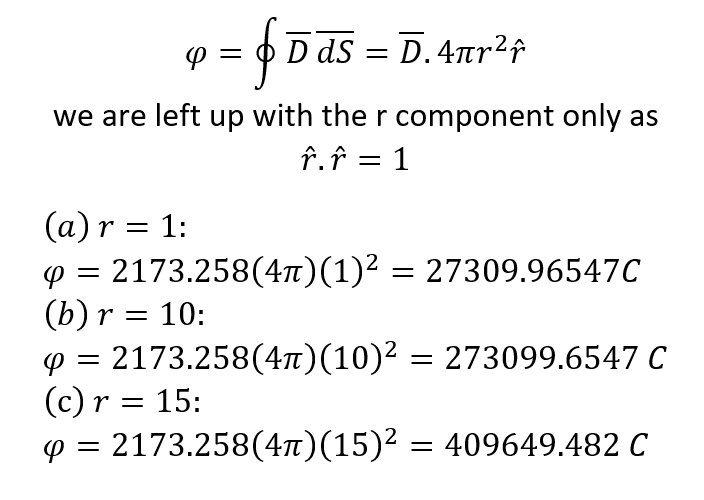Discussion Overview
The discussion revolves around calculating the electric flux through spherical surfaces at specified radii, particularly focusing on the charge enclosed within those surfaces. Participants explore the implications of given values and the interpretation of the problem statement, including the assumptions about the center of the spheres and the units of flux.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants express confusion over the accuracy of results derived from limited significant figures, questioning the validity of achieving high precision from low precision inputs.
- One participant suggests that the total charge enclosed at radius r=1 is -3 µC, based on the position of the charge relative to the sphere.
- Another participant interprets the problem as involving spheres centered at the origin, asserting that the enclosed charge is zero for r=1.
- There is a discussion about the units of flux, with some participants noting that the SI unit for electric flux differs from the units mentioned in the problem.
- Participants debate the relevance of vectors and their lengths in the context of calculating flux, with some seeking clarification on the necessity of certain calculations.
- A later reply indicates that a unit vector is involved in the calculations, but there is uncertainty about its application to the flux problem.
- One participant expresses appreciation for the clarity of an alternative explanation compared to the initial post.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the interpretation of the problem or the calculations involved. Multiple competing views remain regarding the charge enclosed and the appropriate approach to calculating the flux.
Contextual Notes
There are unresolved assumptions about the problem statement, particularly regarding the position of charges and the definition of the spherical surfaces. The discussion also highlights potential confusion over the application of mathematical concepts and units.