Calculating time period of oscillation

[Saitama]

Homework Statement

Homework Equations

The Attempt at a Solution

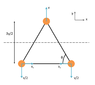
(see attachment 3)
If the middle charge is moved a y distance, then the other two move a distance y/2 in opposite direction. Similarly, the velocity in y direction of other two can be also calculated. As the rods are rigid, the component of velocities along the rod should be equal i.e
v_x\cos \theta-\frac{v}{2}\sin\theta=v\sin\theta \Rightarrow v_x=\frac{3v}{2}\tan\theta
Calculating the energy of system and differentiating it w.r.t time and setting the derivative equal to zero gives the time period.
E=\frac{kq^2}{l}+\frac{kq^2}{l}+\frac{kq^2}{2l\cos\theta}+\frac{1}{2}mv^2+2 \times \frac{1}{2}m(v_x^2+\frac{v^2}{4})
\Rightarrow E=\frac{kq^2}{l}+\frac{kq^2}{l}+\frac{kq^2}{2l\cos\theta}+\frac{3}{4}mv^2+\frac{9mv^2}{4}\tan^2\theta
Since y<<<l,
\frac{1}{\cos\theta}=1/(\sqrt{1-\frac{9y^2}{4l^2}})=1+\frac{9y^2}{8l^2}
I don't understand how should I write $\tan^2\theta$
\tan\theta=\cfrac{\cfrac{3y}{2}}{\sqrt{1-\frac{9y^2}{4l^2}}}
\tan^2\theta=\frac{9x^2}{4}\left(1-\frac{9y^2}{4l^2}\right)^{-1}
\Rightarrow \tan^2\theta = \frac{9x^2}{4}\left(1+\frac{9y^2}{4l^2}\right)
But I don't think substituting this in the energy expression is a good idea because I will end up with terms consisting $v^2x^2$ and $v^2x^4$.

Any help is appreciated. Thanks!

 

[darkxponent]

Oscillations are found for small displacementas. Thake the displacement of middle charge dy. Assume that other two charges don't move.
Then proove that it oscilates in Simple Harmonic motion.

 

[Saitama]

Oscillations are found for small displacementas. Thake the displacement of middle charge dy. Assume that other two charges don't move.
Then proove that it oscilates in Simple Harmonic motion.

What? I had to solve it this way? LOL, I was over thinking on the problem.

Okay, for this type of oscillation, I get:
T=2\pi\sqrt{\frac{ml^3}{2kq^2}}

Is this what you get?

 

[darkxponent]

Well, if i don't know whether there are other ways in which it can osscilates. Your diagrams do not seem to agree with this type of osscilation. But if it oscilates like this then i am also getting same answer as yours.

 

[Saitama]

Well, if i don't know whether there are other ways in which it can osscilates. Your diagrams do not seem to agree with this type of osscilation. But if it oscilates like this then i am also getting same answer as yours.

I plugged in the values and got T=0.0444 but this is wrong.

 

[darkxponent]

I think taking yhe other two charges fixed was wrong. Take them movable, it still is the SHM.

Is the answer pi/10?

 

[Saitama]

I think taking yhe other two charges fixed was wrong. Take them movable, it still is the SHM.

Is the answer pi/10?

How do you get $\pi/10$ (I don't know about the answer)?

If middle charge moves a distance dy, the other two moves a distance dy/2. That will result in a time period of
T=2\pi\sqrt{\frac{ml^3}{3kq^2}}

 

[darkxponent]

How do you get $\pi/10$ (I don't know about the answer)?

If middle charge moves a distance dy, the other two moves a distance dy/2. That will result in a time period of
T=2\pi\sqrt{\frac{ml^3}{3kq^2}}

Look at the diagram given in question, according to that if middle charge moves a distance dy upwards the other two charges mobe a distance dy downwards(as l is constant). Why are you getting dy/2?

 

[Saitama]

Look at the diagram given in question, according to that if middle charge moves a distance dy upwards the other two charges mobe a distance dy downwards(as l is constant). Why are you getting dy/2?

Conservation of linear momentum.

Is it wrong to use it here?

 

[darkxponent]

Conservation of linear momentum.

Is it wrong to use it here?

I am also confused about taking conservation of linear of linear momentum. It violates symmetry and the diagram as there can be other interactions as well I think the the better method would be taking the potential energy as function of 'y' and the finding force. But it is more or less the same.

I think we need help from senior members. I have asked ehild!

 

[voko]

I have not watched the entire discussion, but: have you been able to express the potential and kinetic energies solely in terms of theta and the given constants?

When that is done, linearize the equation expressing conservation of energy assuming theta is small.

It should then be fairly simple to proceed.

 

[Saitama]

I have not watched the entire discussion, but: have you been able to express the potential and kinetic energies solely in terms of theta and the given constants?

When that is done, linearize the equation expressing conservation of energy assuming theta is small.

It should then be fairly simple to proceed.

voko, please check the OP, I have already stated why I am not able to proceed. I have used the same method you are stating (I think). Thanks! :)

 

[voko]

I do not see any attempt or any problem in #1 in expressing $v$ via $\theta$ and $\dot{\theta}$.

 

[Saitama]

I do not see any attempt or any problem in #1 in expressing $v$ via $\theta$ and $\dot{\theta}$.

\sin\theta=\frac{3y}{2l}
x=\frac{2l\sin\theta}{3}
Differentiating w.r.t time
v=\frac{2l\cos\theta}{3} \dot{\theta}

Is this what you ask me?

 

[voko]

Assuming it is correct, yes (sorry, no time to check that now).

Now you have energy in terms of the angle and the angular velocity. Assuming the angle is small, derive an equation quadratic (at most) in them, and that should give you what you want.

 

[Saitama]

Assuming it is correct, yes (sorry, no time to check that now).

Now you have energy in terms of the angle and the angular velocity. Assuming the angle is small, derive an equation quadratic (at most) in them, and that should give you what you want.

For small angle, $tan^2\theta=\theta^2$ and $\cos\theta=1-\theta^2/2$, right?

Please check my energy equation in the first post when you have time, thank you.

 

[TSny]

\Rightarrow E=\frac{kq^2}{l}+\frac{kq^2}{l}+\frac{kq^2}{2l\cos\theta}+\frac{3}{4}mv^2+\frac{9mv^2}{4}\tan^2\theta

Can you argue that the last term on the right is of higher order in the small quantities θ and v and can therefore be neglected?

Since y<<<l,
\frac{1}{\cos\theta}=1/(\sqrt{1-\frac{9y^2}{4l^2}})=1+\frac{9y^2}{8l^2}

Everything looks good to me.

 

[Saitama]

Can you argue that the last term on the right is of higher order in the small quantities θ and v and can therefore be neglected?

I initially thought of neglecting them but I wasn't too sure. I think its okay to do that.

Differentiating the energy equation w.r.t time and setting the derivative equal to zero, I get
T=2\pi\sqrt{\frac{4ml^3}{3kq^2}}
Is this what you get?

 

[TSny]

Yes.

 

[Saitama]

Yes.

Thanks a lot TSny!

 

[ehild]

A slightly different approach:

The problem can be written entirely in terms of θ:

x1=-Lcosθ, y1=Lsinθ/3
x2=Lcosθ, y2=Lsinθ/3
x3=0, y3=-2Lsinθ/3 (middle atom)

These displacements leave the CM stationary.

The velocity components are: x1'=Lsinθθ', y1'=L/3 cosθθ' ...

KE= mL²θ'²(sin²(θ)+cos²(θ)/3)

PE=2kq²/L+kq²/(2Lcosθ)

Supposing maximum angular speed θ' was given initially at θ=0. The KE is zero when the angle is θmax=A

Initial energy: mL²θ'²(1/3)+2kq²/L+kq²/(2L)

Final energy: 2kq²/L+kq²/(2LcosA)

cosA≈1-A²/2 if A is small. 1/(1-A²/2)≈1+A²/2


So we get : mL²θ'²(1/3)=kq²/(2L)A²/2
θ'²=3/4 kq²/(L³m)A² where θ' is the maximum angular speed.

For an SHM, maximum speed = amplitude * ω.

ehild

 

[Saitama]

A slightly different approach:

The problem can be written entirely in terms of θ:

x1=-Lcosθ, y1=Lsinθ/3
x2=Lcosθ, y2=Lsinθ/3
x3=0, y3=-2Lsinθ/3 (middle atom)

These displacements leave the CM stationary.

The velocity components are: x1'=Lsinθθ', y1'=L/3 cosθθ' ...

KE= mL²θ'²(sin²(θ)+cos²(θ)/3)

PE=2kq²/L+kq²/(2Lcosθ)

Supposing maximum angular speed θ' was given initially at θ=0. The KE is zero when the angle is θmax=A

Initial energy: mL²θ'²(1/3)+2kq²/L+kq²/(2L)

Final energy: 2kq²/L+kq²/(2LcosA)

cosA≈1-A²/2 if A is small. 1/(1-A²/2)≈1+A²/2


So we get : mL²θ'²(1/3)=kq²/(2L)A²/2
θ'²=3/4 kq²/(L³m)A² where θ' is the maximum angular speed.

For an SHM, maximum speed = amplitude * ω.

ehild

Thank you ehild! This is much better.