Sagrebella
- 61
- 2
Hello, could someone please check my answer for this problem. All of my work and equations are clearly presented in the picture attached below. (If my answer is wrong, please give me pointers on how I could obtain the correct solution).
Thanks !
Problem 3:
You paddle your canoe at a constant speed of 4.00 km/h relative to the water. You are canoeing along a river that is flowing at a constant speed of 1.10 km/h. If you paddle for 60.0 minutes downstream (with the current) and then turn around, how long does it take you to get back to your starting point?
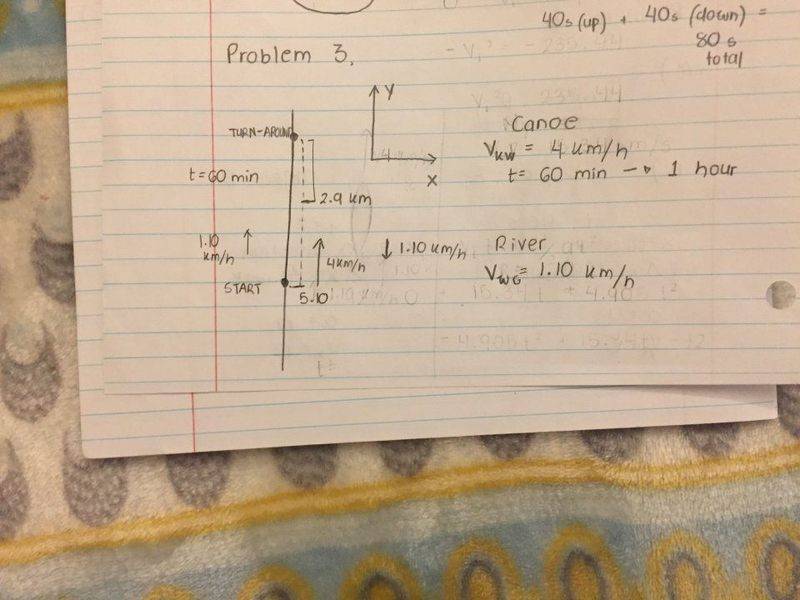
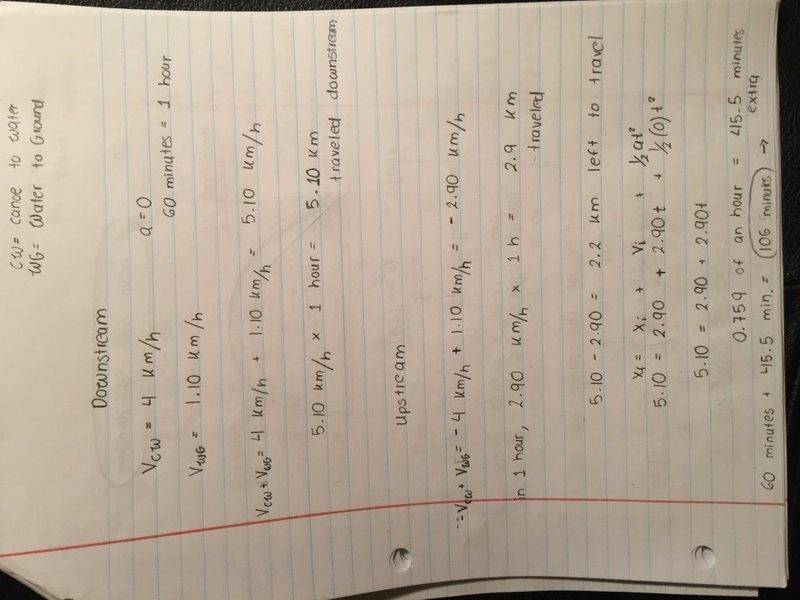
Thanks !
Problem 3:
You paddle your canoe at a constant speed of 4.00 km/h relative to the water. You are canoeing along a river that is flowing at a constant speed of 1.10 km/h. If you paddle for 60.0 minutes downstream (with the current) and then turn around, how long does it take you to get back to your starting point?