Calculating Work: 100N Block on Incline of 37o, 2m Distance

[Saitama]

Homework Statement

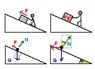
A block of weight 100N is slowly slid up on a smooth incline of inclination 37^o by a person. Calculate the work done by the person in moving the block through a distance of 2m if the driving force is (a) parallel to the incline (b)in the horizontal direction.

Homework Equations

The Attempt at a Solution

I don't understand what should be the driving force?
Should it be 60N because the block is of weight 100N and its sine component is 60N?

 

[JHamm]

The work done moving the block up the slope is the same as the work gravity would do bringing it down that same distance.

 

[Saitama]

The work done moving the block up the slope is the same as the work gravity would do bringing it down that same distance.

Thanks for the reply JHamm but then what should be the driving force for the (b) part?
So if i solve the (a) part, w=120 J. For the part (b) should the driving force be again 60N?

 

[I like Serena]

Hi Pranav! :)

Yes, the work is 120 J, and the force the person would apply parallel to the incline is 60 N.
If the person applies a horizontal driving force, he needs to apply a different force.
Can you set up the equation for equilibrium?

 

[Saitama]

Hello ILS! :)

When force is applied horizontally, the equation for equilibrium is:-
Fcos37^o=60N

From here, i get F=100N. But then what should be the displacement? Should it be 1.2m?

 

[I like Serena]

Work = force in the direction of the displacement $\times$ displacement.

The displacement is still 2 m, the relevant part of the force is still 60 N. ;)

 

[ehild]

I don't understand what should be the driving force?
Should it be 60N because the block is of weight 100N and its sine component is 60N?

It is not explicitly said, but "the block is slowly slid up" indicates, that it does not accelerate and when it started from rest, its acceleration was so small that it does not count. No acceleration means zero resultant force.

ehild

 

[Saitama]

Work = force in the direction of the displacement $\times$ displacement.

The displacement is still 2 m, the relevant part of the force is still 60 N. ;)

Yeah, i know that force in the formula is in the direction of displacement but according to what i said, the displacement is 1.2m in the direction of 100N force. So W=100 X 1.2=120J, which is correct according to the answer key.

It is not explicitly said, but "the block is slowly slid up" indicates, that it does not accelerate and when it started from rest, its acceleration was so small that it does not count. No acceleration means zero resultant force.

ehild

So do you mean work is zero?

 

[netgypsy]

The resultant force is zero, not the force used to move the object up the ramp i.e. the driving force. You don't find the displacement in the horizontal direction unless it is asked for, which it isn't, You use the force you found in part a, then find the total force you would have to exert if your force is horizontal rather than up the ramp. So force horizontal times cosine of the ramp angle will equal the force you already calculated needed to drive the mass up the ramp.

In other words, if you push horizontally rather than along the line of the ramp, you have to push harder to move the object up the ramp

When you calculated the 1.2m and multiplied it by the force horizontal, all you did was verfy that the work done is the same regardless of path, which is true but you aren't asked for the 1.2m so you didn't HAVE to find it to answer the question.

 

[ehild]

Yeah, i know that force in the formula is in the direction of displacement but according to what i said, the displacement is 1.2m in the direction of 100N force. So W=100 X 1.2=120J, which is correct according to the answer key.



So do you mean work is zero?

The resultant of the work of all forces is zero, and the sum of all forces too, but the work of the individual forces is not (except the normal force, its work is always zero). What I said was answer to your question about the driving force. It exactly balances the other forces, gravity and normal force. See picture: the red arrow is the "driving force", F, G is gravity (blue) and N is the normal force (green). When the applied force is parallel to the slope, its magnitude is F_p=Gsin(φ). If the applied force is horizontal, F_h=Gtan(φ). The work is displacement times force times the cosine of the enclosed angle. For the parallel force, the enclosed angle is zero: W=Fd=Gsin(φ)d. The horizontal force encloses φ angle with the slope, so its work is W=Fdcos(φ)=(Gtan(φ))dcos(φ)=Gsin(φ)d: they are equal (120J) and just opposite to the work of gravity -Gsin(φ)d.

ehild

 

[I like Serena]

Yeah, i know that force in the formula is in the direction of displacement but according to what i said, the displacement is 1.2m in the direction of 100N force. So W=100 X 1.2=120J, which is correct according to the answer key.

Yeah, well, it's not only true that:

Work = force in the direction of the displacement × displacement.​

It is also true that:

Work = force × displacement in the direction of the force.​

This is the same thing.


Edit: The force of gravity does negative work.
The force exerted by the person does the same but positive work.

 

[ehild]

Hello ILS! :)

When force is applied horizontally, the equation for equilibrium is:-
Fcos37^o=60N

From here, i get F=100N. But then what should be the displacement? Should it be 1.2m?

F=60/cos(37)=75 N, not 100.

ehild

 

[netgypsy]

need to get a slide rule :-)

 

[Saitama]

The resultant of the work of all forces is zero, and the sum of all forces too, but the work of the individual forces is not (except the normal force, its work is always zero). What I said was answer to your question about the driving force. It exactly balances the other forces, gravity and normal force. See picture: the red arrow is the "driving force", F, G is gravity (blue) and N is the normal force (green). When the applied force is parallel to the slope, its magnitude is F_p=Gsin(φ). If the applied force is horizontal, F_h=Gtan(φ). The work is displacement times force times the cosine of the enclosed angle. For the parallel force, the enclosed angle is zero: W=Fd=Gsin(φ)d. The horizontal force encloses φ angle with the slope, so its work is W=Fdcos(φ)=(Gtan(φ))dcos(φ)=Gsin(φ)d: they are equal (120J) and just opposite to the work of gravity -Gsin(φ)d.

ehild

Oh ok, i see now.
Thanks for the help ehild!

Yeah, well, it's not only true that:

Work = force in the direction of the displacement × displacement.​

It is also true that:

Work = force × displacement in the direction of the force.​

This is the same thing.


Edit: The force of gravity does negative work.
The force exerted by the person does the same but positive work.

Yeah, ehild explained in his previous post.
Thanks!

F=60/cos(37)=75 N, not 100.

ehild

I am sorry.

 

[sankalpmittal]

Oh ok, i see now.
Thanks for the help ehild!
Yeah, ehild explained in his previous post.
Thanks!
I am sorry.

These questions can be done much easily if you draw the diagrams of the force acting on a block correctly. Your geometry should be correct and you must resolve the correct components of the force. In this straightforward question it is easily stated that first tell the force in the horizontal direction which is horizontal component of force. Using Pythagoras theorem you can then find the force parallel to the incline OR just divide your answer to previous part by cosθ. The slope of the two components can be determined by tanθ.

 

[netgypsy]

The drawings are critical for problems of this type. If they are done correctly you will almost always get them right.