Calculating Work Done by Varying Force on a Moving Block - Easy Physics Problem

[DizBelieF14]

I honestly feel like a complete idiot asking this, since I know it's really easy, but I just can't get the answer. The question is...

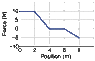
A 3.0 kg block moves in a straight line on a horizontal frictionless surface under the influence of a force that varies with position as shown in Figure 7-38 (attached). How much work is done by the force as the block moves from the origin to x = 8.0 m?

I thought this problem was as simple as finding the area under the curve, because it's force versus distance. Doing this, I got -45 because the bottom of the graph goes into the negatives (or 105 if negatives don't mean anything). Neither of these answers are correct (using WebAssign for homework), and I can't figure out why. Am I just being really stupid with the math? Does the mass even matter, I thought it didn't because you're just integrating? Sorry for the stupid question, I just don't have anyone else to ask... :shy:

 

[radou]

I can't see the attachment, but basically, the work should be W = \int_{0}^8 F(x)dx, where F(x) is your graph. The integral actually equals the change in potential, U(8) - U(0), where the potential U(x) is the antiderivative of F(x).

 

[rsk]

Can you give us an expression for F - given that we can't see the attachment yet?

You must have one, to be able to integrate? Or is your graph just straight lines?

 

[DizBelieF14]

It is simply a graph with straight lines. I thought that you simply break them up into rectangles and triangles and just add the areas..I really hope my simple math is just wrong, because otherwise I have no idea..Heres the direct link to the graph.

http://www.webassign.net/hrw/07_33.gif

 

[rsk]

It must be your maths. I can't get 105 or 45 no matter what.

Remember you´re taking the areas around the F=0 line.

 

[DizBelieF14]

Oh, around the 0? Okay, 25, I got it. I thought you just took it to the bottom of the graph itself. Sorry for the stupid question, I am a freshman in high school in physics, so I don't pick up on this stuff easily by myself. Thank you very much.

 

[rsk]

Easy mistake from the way that graph is drawn!

 

[radou]

Oh, around the 0? Okay, 25, I got it. I thought you just took it to the bottom of the graph itself. Sorry for the stupid question, I am a freshman in high school in physics, so I don't pick up on this stuff easily by myself. Thank you very much.

There are no stupid questions.

 

[rsk]

But there are, at times, stupidly presented graphs... ;)