Calculation of Kinetic Energy in Rotation Motion

[Amartya Sen]

Homework Statement

Respected Physics Gurus/experts...!

I am confused in the application of Kinetic energy Expression, i.e, KE = (1/2)MV_CM²+(1/2)I_CMω²
I had been trying out this question actually(it's pretty simple though)...---

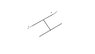
"A rigid body is made of three identical thin rods each of length L fastened together in the form of letter H. The body is free to rotate about a fixed horizontal axis AB that passes through one of the legs of the 'H'. The body allowed to fall from rest in a position in which the plane of H is horizontal. What is the angular speed of the body, when the plane of H is vertical?

https://physicsforums-bernhardtmediall.netdna-ssl.com/data/attachments/80/80350-15ec1ccefce05dd0a160c18183367070.jpg

Homework Equations

KE = (1/2)MV_CM²+(1/2)I_CMω²[/B]
& Work Energy Theorem

The Attempt at a Solution

I tried by considering the whole H at it's centre of mass and the applied the formulae but the answer I got was incorrect. My friend told me that since the 'H' is only rotating, the (1/2)MVCM2 term could be neglected...Why is it so? The CM has some velocity afterwards... Although the correct answer can be obtained by following this approach
Any help would be appreciated..!

 

[Doc Al]

My friend told me that since the 'H' is only rotating, the (1/2)MVCM2 term could be neglected...Why is it so?

You can treat the body as purely rotating, but if you do, make sure you use the rotational inertia about the axis of rotation, not the center of mass.

 

[Amartya Sen]

I know that...But why it is so..? And what's wrong with the application of the original formula?

 

[BvU]

Hello Amartya,

If you look carefully at the definition of moment of inertia -- in this case about an axis not through the center of mass -- you can see that the kinetic energy of the center of mass is already accounted for. To check you can work it out for a simple point mass instead of for an extended object.

There is a theorem - the parallel axis theorem, which google -- that links the moment of inertia around an axis through the center of mass to the moment of inertia around a parallel axis NOT through the center of mass

 

[Amartya Sen]

If you look carefully at the definition of moment of inertia -- in this case about an axis not through the center of mass -- you can see that the kinetic energy of the center of mass is already accounted for. To check you can work it out for a simple point mass instead of for an extended object.

There is a theorem - the parallel axis theorem, which google -- that links the moment of inertia around an axis through the center of mass to the moment of inertia around a parallel axis NOT through the center of mass

Thanks BvU for your help..!
In the first place, I do know the parallel+perpendicular axis theorems.

But the formula says that we have to use the MoI about the COM of the object, not about the axis about which it is rotating.
Saying this, I want to also add that it's unclear that if we do have to use MOI about COM, so which plane we have to use?? ( As in this case---I think its the axis about which the direction of original rotation remains changed)
Next, I have used the formula exactly as it is in other questions regarding which there are no complaints...

Man, I do feel sometimes dizzy regarding some concepts in rotational motion..(toughest chapter for me)
It makes me go ...

Plz, lead me out of trouble..

 

[BvU]

No problem. Show your calculations and someone will point out where things go awry -- if at all (sometimes book answers can be wrong too). In your case, friend is wrong (or misquoted...).

 

[Amartya Sen]

Here's my solution anyway...

Considering the body to be centred at the mid point of the middle leg of the 'H', we have,

mgl/2 =mv²/2 + [(ml²/12 + ml²/4 + ml²/4)ω²]/2
which on simplifying and putting v=ωl/2 gives:
ω=(12g/17l)^0.5

Totally wrong.

 

[Doc Al]

But the formula says that we have to use the MoI about the COM of the object, not about the axis about which it is rotating.

But you don't have to use that formula. (But you can if you wish.)

mgl/2 =mv²/2 + [(ml²/12 + ml²/4 + ml²/4)ω²]/2

Does "m" stand for the total mass? Your expression for MOI is not clear.

 

[BvU]

Problem statement says three identical rods of length L. From your $I_{\rm c.o.m.}$ I gather each rod has mass m. In that case there should be a 3 mgL/2 = 3 mv²/2 + ... on the left !

And you can quickly check this parallel axis theorem as well.

 

[Amartya Sen]

Oh Yeah..Yeah...I'm sorry. It should be as BvU said. Thanks BvU..
Anyway, even after the correction, answer comes to be wrong...

 

[BvU]

How can you tell that the answer is wrong ?

 

[Amartya Sen]

Yahoo...Finally I arrived the answer...It turns out that I had been replacing v² by ω²l² instead of ω²l²/4 in the final step ...

Thanks pals... And sorry for wasting your precious time..if I did.