Calculations: Creep of Metals and the Life of a Rod

[Nadia]

TL;DR

Exercise about estimating the life of a rod given a graph and an equation to work with. (Ex. 3.6 from Inelastic Deformation of Metals: Models, Mechanical Properties, and Metallurgy from D. C. Stouffer and L. Thomas Dame)

I'm sorry I'm uploading lots of images because I don't know how to write equations here.

PROBLEM DESCRIPTION

I have to solve this problem:

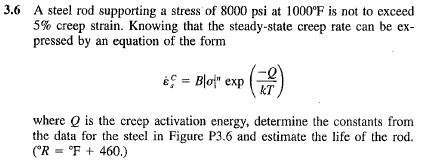
Figure P3.6:

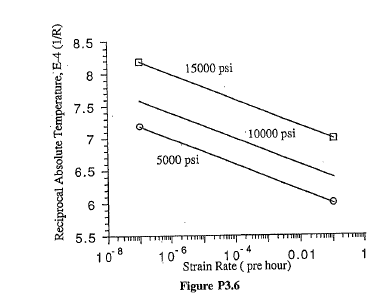
MY SOLUTION

I did this:

THE CORRECTION

I got this as a correction:

- Don't use the middle line in figure P3.6 in my calculations.
- Start finding Q/k but for the top and bottom line, if they are not identical, deal with it.
- You will now have the temperature dependance.
- Plot ln(eps-dot)+Q/kT as a function of ln(Sigma)
- You get two points from which you can calculate n and B

SOLUTION AFTER THE CORRECTION

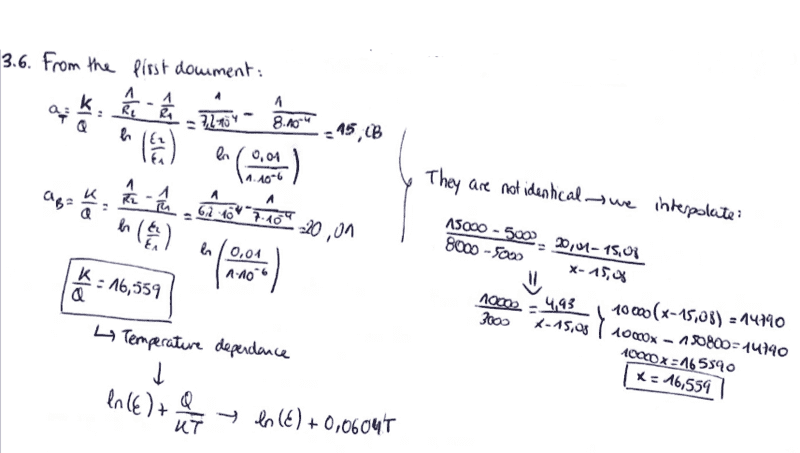
I've now done this part but I think it's wrong and I also don't know how to keep going with the plot.

 

[FEAnalyst]

It's hard to read those hand notes. It would certainly help if you rewrote the equations using LaTeX: https://www.physicsforums.com/help/latexhelp/

 

[Nadia]

It's hard to read those hand notes. It would certainly help if you rewrote the equations using LaTeX: https://www.physicsforums.com/help/latexhelp/

Okay! Thanks, I didn't see this. I'm gonna give it a try

 

[Nadia]

It's hard to read those hand notes. It would certainly help if you rewrote the equations using LaTeX: https://www.physicsforums.com/help/latexhelp/

I managed more or less.

The new thread using LaTeX is here:
https://www.physicsforums.com/threads/creep-of-metals-2.1048883/

<Moderator's note: the threads have been merged, see post below.>

 

[Nadia]

In this thread, the problem is presented using images:

https://www.physicsforums.com/threads/creep-of-metals.1048878/

PROBLEM DESCRIPTION

I have to solve this problem:

3.6 A steel rod supporting a stress of 8000 psi at 1000ºF is not to exceed 5% creep strain. Knowing that the steady-state creep rate can be expressed by an equation of the form
$$ε = B|∂|^n exp (-Q/kT)$$,

where Q is the creep activation energy, determine the constants from the data for the steel in Figure P3.6 and estimate the life of the rod. (ºR = ºF - 460).

Figure P3.6:

MY SOLUTION
$y = ax+b$, $a=\frac {\Delta y} {\Delta x} = \frac {y_2-y_1} {ln(\frac {x_2} {x_1})}$
$$ε = B|∂|^n exp (-Q/kT),$$

$1/T=m ln ε + n$

$lnε=lnB+nln|∂|-Q/(kT) \rightarrow lnε -b = \frac {-Q} {k} · \frac {1} {T}$
$\rightarrow \frac {-k} {Q} · \{ lnε - lnb \} = \frac {1} {T}$
$\rightarrow \frac {k} {Q} lnb - \frac {k} {Q} lnε = \frac {1} {T}$
$\rightarrow a = \frac {k} {Q} = \frac {\frac {1} {R_2} - \frac {1} {R_1}} {ln (\frac {ε_2} {ε_1}) }$

Using points from the graph:

$a = \frac {k} {Q} = \frac {\frac {1} {6.5*10^{-4}} - \frac {1} {6.85*10^{-4}}} {ln (\frac {0.006} {0.0008}) }=3.901*10^{-7}$

$\rightarrow ln0.0008 · lnB+n ln 8000 - \frac {1} {3.901*10^{-7}} · \frac {1} {811}$

$\rightarrow ln0.0008 + \frac {1} {3.901*10^{-7}} · \frac {1} {811} -n ln8000 = lnB$

$ln0.0003=lnB + n ln5000 - \frac {1} {3.901*10^{-7}} · \frac {1} {T_2}$,

where $\frac {1} {R} = 6.5*10^{-4} \rightarrow F = 1078,46 \rightarrow T_2 = 855K$

$ln0.0003=lnB + n ln5000 - \frac {1} {3.901*10^{-7}} · \frac {1} {855}$

$ln0.0003+\frac {1} {3.901*10^{-7}} · \frac {1} {855}-n ln5000=lnB$

$ln0.0008+\frac {1} {3.901*10^{-7} · 811} -n ln8000=ln0.0003+\frac {1} {3.901*10^{-7}} · \frac {1} {855}-n ln5000$

$3153.71-n ln8000 = 2990.07-n ln5000$

$163.64 = n ln8000 - n ln5000= n (ln8000-ln5000) = n 0.47$

$n = \frac {163.64} {0.47} = 348.16$

$-> ln0.0003 + \frac {1} {3.901*10^{-7} · 855} - 348.16 · ln5000 = lnB \rightarrow 24,6598 = lnB$

$e^{24.6598} = e^{lnB} = B \rightarrow B = 5.124 * 10^{10}$

From the relationship between strain rate and time:
$ln t = lnε + \frac {Q} {kT} - n ln∂ - lnB = 0.064$

$\rightarrow t=e^{0.064} = 1.067$

THE CORRECTION

I got this as a correction:

- Don't use the middle line in figure P3.6 in my calculations.
- Start finding Q/k but for the top and bottom line, if they are not identical, deal with it.
- You will now have the temperature dependance.
- Plot ln(eps-dot)+Q/kT as a function of ln(Sigma)
- You get two points from which you can calculate n and B

SOLUTION AFTER THE CORRECTION
From the first document:

$a_T = \frac {k} {Q} = \frac {\frac {1} {R_2} - \frac {1} {R_1}} {ln (\frac {ε_2} {ε_1})} = \frac {\frac {1} {7.2*10^{-4}} - \frac {1} {8*10^{-4}}} {ln (\frac {0.01} {1*10^{-6}}) } = 15.08$

$a_B = \frac {k} {Q} = \frac {\frac {1} {R_2} - \frac {1} {R_1}} {ln (\frac {ε_2} {ε_1})} = \frac {\frac {1} {6.2*10^{-4}} - \frac {1} {7*10^{-4}}} {ln (\frac {0.01} {1*10^{-6}}) } = 20.01$

They are not identical, so we interpolate:

$\frac {15000-5000} {8000-5000} = \frac {20.01-15.08} {x-15.08}$

From where $x = 16.559$
$\frac {k} {Q} = 16.559$ temperature dependance -> $ln(ε) + \frac {Q} {kT} -> ln(ε) + 0.0604/T$