Calculations using the Standard Solar Model & Solar Equations of State

[dzizzling]

Homework Statement

- I have to determine the density at the centre of the Sun, compare this with the mean density of the core, and to comment on the result.

- I have to determine the density of the white dwarf, Sirius B, whose mass, M = 1 M_solar_mass, and radius, r = 0.008 R_solar_radius, to compare it with the density of the Sun’s core, and to comment on the result.

- I have to determine the density at the surface of the core of the Sun. Using this density i have to calculate the rate of change of pressure with radius at that surface.

- I have to determine the mean energy generation rate per unit mass of the core 𝜀.

Relevant Equations

[Task a.]
- The mass distribution equation as ordinary differential equation:

$$\frac{dM(r)}{dr} = 4 \pi r^2 \rho(r)$$

and as integration:

$$m(r) = \int^r_0 4 \pi r^2 \rho dr$$

yields the mass m(r) inside a spherical shell of radius r. This equation describes the mass M(r) contained within a radius r in terms of the mass density ρ (rho).]
----------------------------------------

[Task c.]
- The pressure within the Sun is then given by:

$$P(r) = \frac{\rho(r)}{\mu m_H} kT(r)$$
, with

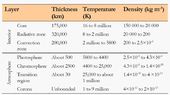
- ρ = 2.45e4 kg m-3, is the density at the surface of the core at R = 0.25 Rsolar_radius
- μ = 0.5, is the mean molecular weight for the gas,
- mH = 1.67e-27 kg, is the mass of a hydrogen atom,
- k = 1.38×10−23 J K-1, is Boltzmann’s constant
- 𝑇(𝑟) = 8e6 K, is the temperature at radius 𝑟,
----------------------------------------

[Task d.]
- The equation of stellar structure for the energy generation which is rearranged to the normal form:
$$\frac{dL(r)}{dr} = 4 \pi r^2 \rho(r) \epsilon(r)$$

to get 𝜀 the energy generation per unit mass, with

- 𝐿(𝑟) is the luminosity within the Sun at radius 𝑟,
- r = 0.25 Rsolar_radius is the radius of the solar core,
- dr is the spherical shell where the energy generation happens,
- ρ = 2.45e4 kg m-3, is the density at the surface of the core at R = 0.25 Rsolar_radius].

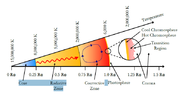
Assuming the Sun’s core has a mass of 0.35 Msolar_mass and taking values for other quantities from a internet background search or from the following figures
(i.e.: Radius "solar core" = 0.25 Rsolar_radius ):
------------------------------------------------------------------------
------------------------------------------------------------------------

a.
Determine the density at the centre of the Sun.
Compare this with the mean density of the core.
Comment on the result.

[Hint 1: Its not about the density at R=0, which may confuse a bit as mass inside a sphere of radius R=0 is of course 0. But density is defined as mass per unit volume: You can imagine a small volume at the centre of the Sun, having mass.]

[Hint 2: You can use an derivative (i.e. an second order differential equation) of one of the "equations of stellar structure" to solve this question.
I.e.: The mass distribution equation as ordinary differential equation

$$\frac{dM(r)}{dr} = 4 \pi r^2 \rho(r)$$

and as integration:

$$m(r) = \int^r_0 4 \pi r^2 \rho dr$$

yields the mass m(r) inside a spherical shell of radius r. This equation describes the mass M(r) contained within a radius r in terms of the mass density ρ (rho).]
------------------------------------------------------------------------

b.
Determine the density of the white dwarf, Sirius B, whose mass, M = 1 Msolar_mass, and radius, r = 0.008 Rsolar_radius.
Compare it with the density of the Sun’s core.
Comment on the result.
------------------------------------------------------------------------

c.
Determine the density at the surface of the core of the Sun.
Using this density, calculate the rate of change of pressure with radius at that surface.
[Hint: The pressure within the Sun is then given by

$$P(r) = \frac{\rho(r)}{\mu m_H} kT(r)$$

, with
- ρ = 2.45e4 kg m-3, is the density at the surface of the core at R = 0.25 Rsolar_radius
- μ = 0.5, is the mean molecular weight for the gas,
- mH = 1.67e-27 kg, is the mass of a hydrogen atom,
- k = 1.38×10−23 J K-1, is Boltzmann’s constant
- 𝑇(𝑟) = 8e6 K, is the temperature at radius 𝑟,
[Hint: You will need to make use of the core density from part (a)]
------------------------------------------------------------------------

d. Determine the mean energy generation rate per unit mass of the core 𝜀.
[Hint:
Using the equation of stellar structure for the energy generation which is rearranged to the normal form

$$\frac{dL(r)}{dr} = 4 \pi r^2 \rho(r) \epsilon(r)$$

to get 𝜀 the energy generation per unit mass, with
- 𝐿(𝑟) is the luminosity within the Sun at radius 𝑟,
- r = 0.25 Rsolar_radius is the radius of the solar core,
- dr is the spherical shell where the energy generation happens,
- ρ = 2.45e4 kg m-3, is the density at the surface of the core at R = 0.25 Rsolar_radius].

 

[member38644]

a. To determine the density at the center of the Sun, we can use the equation of stellar structure for mass distribution as shown in the hint provided:

$$m(r) = \int^r_0 4 \pi r^2 \rho dr$$

We can plug in the values given in the question, where M = 0.35 Msolar_mass and r = 0.25 Rsolar_radius. Solving for ρ, we get:

$$\rho (r) = \frac{3M}{4\pi r^3} = \frac{3(0.35 Msolar_mass)}{4\pi (0.25 Rsolar_radius)^3} = 1.68 \times 10^{13} kg/m^3$$

This is the density at the center of the Sun. To compare it with the mean density of the core, we need to calculate the mean density using the equation:

$$\bar{\rho} = \frac{M}{(4/3)\pi r^3} = \frac{0.35 Msolar_mass}{(4/3)\pi (0.25 Rsolar_radius)^3} = 1.96 \times 10^{13} kg/m^3$$

We can see that the mean density of the core is slightly higher than the density at the center. This is because the density of the core decreases as we move towards the surface, whereas the density at the center remains constant. This result is expected as the core is the densest part of the Sun.

b. To determine the density of the white dwarf Sirius B, we can use the equation for mean density:

$$\bar{\rho} = \frac{M}{(4/3)\pi r^3} = \frac{1 Msolar_mass}{(4/3)\pi (0.008 Rsolar_radius)^3} = 1.95 \times 10^{10} kg/m^3$$

Comparing this with the density of the Sun's core, we can see that the density of Sirius B is much lower. This is because white dwarfs are formed from the core of a star after it has exhausted its nuclear fuel, causing it to collapse and become denser. However, Sirius B is still a relatively dense object compared to other celestial bodies.

c. To determine the density at the surface of the core of the Sun, we can use