Calulate the energy stored in capacitor

In summary, a capacitor is an electronic component that stores and releases electrical energy in the form of an electric charge. The energy is stored in a capacitor through the accumulation of positive and negative charges on two conductive plates separated by a dielectric. The formula for calculating the energy stored in a capacitor is E = 1/2 * C * V^2, where E is energy in joules, C is capacitance in farads, and V is voltage in volts. The energy stored in a capacitor is directly proportional to its capacitance, and factors such as voltage and dielectric material can also affect it.
  • #1
noname1
134
0
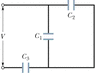
a potential difference V = 100 V is applied across a capacitor arrangement with capacitances C1 = 12.0 µF, C2 = 6.00 µF, and C3 = 16.0 µF. Find the following values.

i calculated cnet and got 847e-6f
voltages across c1 and c2 i got 47.1

now i have to calulate the energy stored in capacitor 1

u = .5 x c x v^2
u = .5 x 12e-6 x 47.1^2 = 0.013J

but i am getting the answer is wrong can anyone confirm?
 

Attachments

  • hrw7_25-28.gif
    hrw7_25-28.gif
    1.5 KB · Views: 459
Last edited:
Physics news on Phys.org
  • #2


How did you get cnet? C1 and C2 are in parallel, and effective capacitance of 1 and 2 is in series with C3.
 

FAQ: Calulate the energy stored in capacitor

What is a capacitor?

A capacitor is an electronic component that stores and releases electrical energy in the form of an electric charge. It is made of two conductive plates separated by an insulating material, known as a dielectric.

How is the energy stored in a capacitor?

The energy is stored in a capacitor in the form of an electric field between the two plates. When a voltage is applied, one plate accumulates positive charge while the other accumulates negative charge, creating the electric field.

What is the formula for calculating the energy stored in a capacitor?

The formula for calculating the energy stored in a capacitor is E = 1/2 * C * V^2, where E is energy in joules, C is capacitance in farads, and V is voltage in volts.

How does the capacitance affect the energy stored in a capacitor?

The higher the capacitance, the more charge can be stored on the plates, resulting in a higher amount of energy stored in the capacitor. Therefore, the energy stored in a capacitor is directly proportional to its capacitance.

What factors can affect the energy stored in a capacitor?

The energy stored in a capacitor can be affected by the capacitance, voltage, and dielectric material. The type of dielectric used can also impact the amount of energy that can be stored in a capacitor.

Similar threads

Capacitors in Series and Parallel
Replies
1
Views
3K
Stored energy among a capacitor arrangement
Replies
4
Views
2K
Energy stored in Capacitor Network
Replies
2
Views
12K
Non-Complex Capacitor Potential Difference question
Replies
9
Views
2K
Capacitor Questions Charging and Discharging
Replies
4
Views
2K
Heat dissipated in a Resistor-Capacitor circuit
Replies
9
Views
2K
Charge and voltage of capacitors?
Replies
4
Views
12K
Energy in capacitor at steady state
Replies
10
Views
2K
Comparing energy lost by the battery & energy gained by the capacitor.
Replies
5
Views
1K
Find the maximum potential difference across a series circuit
Replies
11
Views
3K

Hot Threads

Recent Insights

Back
Top