Jhenrique
- 676
- 4
If a repeated integral can be expressed how an unique integral:
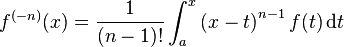
https://en.wikipedia.org/wiki/Cauchy_formula_for_repeated_integration
So is possible express the nth derivative with an unique differentiation?
https://en.wikipedia.org/wiki/Cauchy_formula_for_repeated_integration
So is possible express the nth derivative with an unique differentiation?