Helios
- 267
- 63
- TL;DR Summary
- A Square to Unfolded Cube Geometric Dissection
Dear Recreational Geometry People,
I recovered a thing I did very long ago from a drawing of mine that I fortunately just found again. With some effort I was able reconstruct what I did and redraw it. It is a geometric dissection. The task is to slice up a square and use those pieces to make a unfolded "net" for a cube. I did it in just 4 pieces!
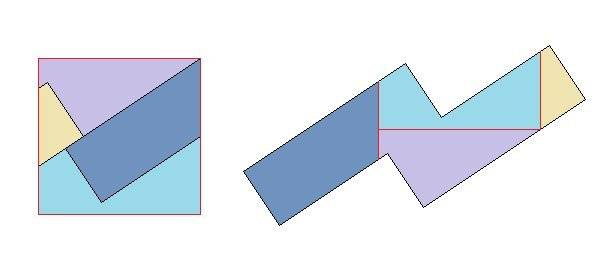
I recovered a thing I did very long ago from a drawing of mine that I fortunately just found again. With some effort I was able reconstruct what I did and redraw it. It is a geometric dissection. The task is to slice up a square and use those pieces to make a unfolded "net" for a cube. I did it in just 4 pieces!