Can Bernoulli's Equation Ensure Fish Safety in Dam Designs?

[Shuff]

I'm doing a project for my University. Making a design for a fish friendly dam structure that will let fish pass downstream without getting through the turbine.

Quick sketch:

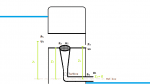
(1/2 u_1^2+p_1+gz_1 )_inlet=(1/2 u_2^2+p_2+gz_2 )_funnel+(1/2 u_3^2+p_3+gz_3 )_fishway

(1/2 u_2^2+p_2+gz_2 )_funnel=(1/2 u_4^2+p_4+gz_4 )_(turbine exit)

These are the two Bernoulli equations I have set up. Are they useable for this case?
If p1 is 20 meters under water surface, can one apply the basic 1 bar per 10meters, or will the water flow u1 play a major role on the p1?

p=F/A=(m⋅g)/A=(V⋅ρ⋅g)/A=(h⋅A⋅ρ⋅g)/A=ρ⋅g⋅h

Can p3 be assumed to be 1atm since it is so close to free air?

Also, how can p2 be calculated/assumed?

The problem I’m having is that I have too many unknowns. The u1 has to be assumed/given, but how can I calculate both u2 and u3. I guess the percentage of the area in the funnel and the fish tunnel ratio is not precise enough to calculate the ratio (funnel has ex. 80% more area than fishway so it has 4 times more flow). Since they are not located the same distance etc.

 

[member 553083]

The Bernoulli equations can be used for this case but you will need additional information to solve them. You will need to know the values of u1, u2, u3, and p1. You can calculate p3 by assuming it is 1 atm since it is close to free air. You can calculate p2 using the hydrostatic pressure equation, which is p=ρgH where p is the pressure, ρ is the density of water, g is the acceleration due to gravity, and H is the height of the liquid column. In order to calculate u2 and u3, you will need to know the area of the funnel and the fishway, as well as their distances from the turbine exit. Using these values, you can calculate the ratio of velocities between the two areas (u2/u3). Then, you can use the Bernoulli equations to calculate the velocities of each section.