You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Can Calculus Problems be Solved by Factoring?
- Thread starter carl binney
- Start date
AI Thread Summary
The discussion revolves around the differentiation of the function y = (2x-5)^3 (x+3)^6 and the challenges faced in factoring the resulting expression. Participants emphasize the importance of clearly presenting mathematical work rather than using images, as this aids in identifying errors. The correct application of the product rule is highlighted, along with the need to factor out the greatest common factor (GCF) from the resulting terms. A detailed example illustrates how to identify and factor the GCF effectively. The conversation underscores that mastering calculus often requires a solid understanding of algebraic principles.
Physics news on Phys.org
Mark44
Mentor
- 38,039
- 10,522
The 2nd line in your attempt is wrong. If you had posted the work itself rather than an image of your work, I could show you exactly where you went wrong. That's why we insist that you post your work directly here, not just post an image.carl binney said:Homework Statement
View attachment 81835 [/B]
hi could some body please help me factorise this please ? any chance of a few stages would be much appreciated
Homework Equations
The Attempt at a Solution
my attempt , but my solutions say otherwise ?
View attachment 81836 [/B]
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
There really is no problem statement here, just a mathematical expression which looks suspiciously like it's the the result of a botched attempt at applying the product rule, and perhaps the chain rule.carl binney said:Homework Statement
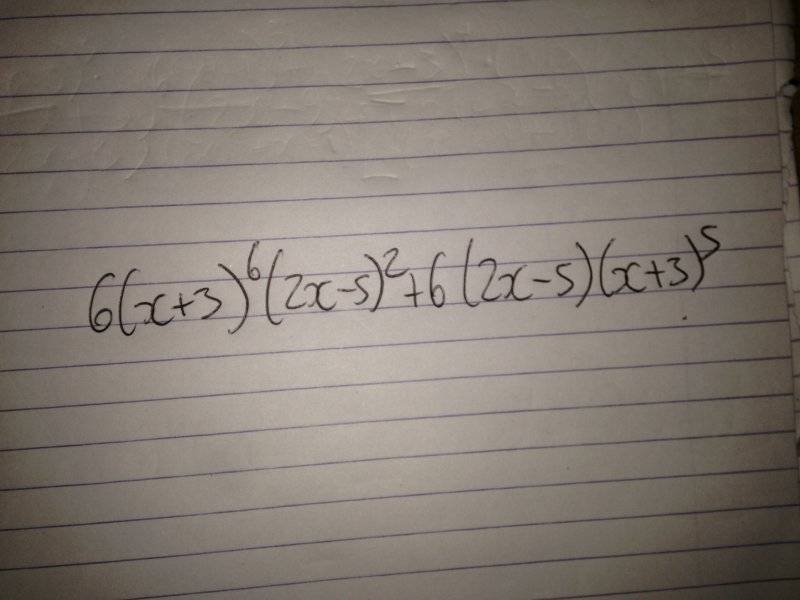
[/B]
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Dear Carl,
I get the impression you didn't read the guidelines as I asked you to do in your first thread. The two replies above should indicate to you that a different approach is in order: after all, if you don't want to be bothered with typing out something simple like
6(x+3)6 (2x-5)2 + 6(x+3)5 (2x-5)
then why should a PhD or MSc who makes his/her precious time available to help others bother to even read your postings ? (which, to be sure, are at least upright and clearly legible -- I've seen a lot worse).
Back to business: as Mark wrote, your second line is a re-write of only the first term (with a 6 too many)
I get the impression you didn't read the guidelines as I asked you to do in your first thread. The two replies above should indicate to you that a different approach is in order: after all, if you don't want to be bothered with typing out something simple like
6(x+3)6 (2x-5)2 + 6(x+3)5 (2x-5)
then why should a PhD or MSc who makes his/her precious time available to help others bother to even read your postings ? (which, to be sure, are at least upright and clearly legible -- I've seen a lot worse).
Back to business: as Mark wrote, your second line is a re-write of only the first term (with a 6 too many)
carl binney
- 7
- 0
hi sorry about the mistakes, the question is
differentiate , y = (2x-5)^3 (x+3)^6
I can get up to where you have to factor the equation, but am unsure what to do from there , any help would be much appreciated ??
differentiate , y = (2x-5)^3 (x+3)^6
I can get up to where you have to factor the equation, but am unsure what to do from there , any help would be much appreciated ??
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
Do things a step at a time. Differentiation (taking derivatives) is a very methodical process.carl binney said:hi sorry about the mistakes, the question is
differentiate , y = (2x-5)^3 (x+3)^6
I can get up to where you have to factor the equation, but am unsure what to do from there , any help would be much appreciated ??
First use the product rule.
What form of the product rule do you use?
carl binney
- 7
- 0
= (x+3)^6 * (3(2x-5)^2*2) + (2x-5)^3 * (6(x+3)^5)
= (x+3)^6 *(6(2x-5)^2) + (2x-5)^3 * (6(x+3)^5)
= 6(x+3)^6 (2x-5)^2+ 6(2x-5) (x+3)^5
factoring this part is where I get stuck ?
= (x+3)^6 *(6(2x-5)^2) + (2x-5)^3 * (6(x+3)^5)
= 6(x+3)^6 (2x-5)^2+ 6(2x-5) (x+3)^5
factoring this part is where I get stuck ?
Mark44
Mentor
- 38,039
- 10,522
carl binney said:differentiate , y = (2x-5)^3 (x+3)^6
You have a mistake in the line above. The exponent on 2x - 5 in the 2nd term should be 3, not 1.carl binney said:= (x+3)^6 * (3(2x-5)^2*2) + (2x-5)^3 * (6(x+3)^5)
= (x+3)^6 *(6(2x-5)^2) + (2x-5)^3 * (6(x+3)^5)
= 6(x+3)^6 (2x-5)^2+ 6(2x-5) (x+3)^5
carl binney said:factoring this part is where I get stuck ?
From your last correct step you have y' = 6(x + 3)6(2x - 5)2 + 6(2x - 5)3(x + 3)5.
You have two terms here, the large expressions that are connected with '+'. Both terms have a factor of 6, so that will be part of the greatest common factor (GCF). Both terms have at least one factor of (x + 3). The GCF will have (x + 3) to the smaller of the two powers that are present in the two terms.
Also both terms have at least one factor of (2x - 5). The GCF will have (2x - 5) to the smaller of the two powers that are present in the two terms.
After you figure out what the GCF is, factor it out of both of the large terms. The other factor will consist of two simpler terms (connected with '+'. Your earlier work was incorrect, in part, because it was missing the '+' between the remaining terms after you factored out the GCF.
As an example, suppose you have ##6x^3y^2 + 12x^2y^4##. Here we have two terms. The GCF has 6 in it, because 6 divides the coefficients of each of the two terms. One term has x3 and the other term has x2. The smaller of these two exponents is 2, so the GCF will include x2. Finally, the first term has y2 and the second term has y4. The smaller exponent is 2, so the GCF must include y2.
From this, we see that the GCF is 6x2y2. We proceed as follows:
##6x^3y^2 + 12x^2y^4 = 6x^2y^2(x + 2y^2)##
As a quick check, expand what is shown on the right, and you should get the expression on the left side.
epenguin
Science Advisor
- 3,637
- 1,013
carl binney said:hi sorry about the mistakes, the question is
differentiate , y = (2x-5)^3 (x+3)^6
I can get up to where you have to factor the equation, but am unsure what to do from there , any help would be much appreciated ??
carl binney said:= (x+3)^6 * (3(2x-5)^2*2) + (2x-5)^3 * (6(x+3)^5)
= (x+3)^6 *(6(2x-5)^2) + (2x-5)^3 * (6(x+3)^5)
= 6(x+3)^6 (2x-5)^2+ 6(2x-5) (x+3)^5
factoring this part is where I get stuck ?
WHERE, where, where?
The factorisation is very obvious to me, RHS of results has the same bracketed terms just to different powers appearing in each of the terms that are added, so each of those terms.to the lower power is a factor of the whole.
However it is true that not only logic but familiarity and practice count in math so this may not be obvious to you.
So make it easier for yourself.
You must have heard in mathematical discourses the term 'WHERE' used. A long complicated mathematical expression is written shorter, saying 'WHERE' some letter is equal to something more complicated, such as w = some complicated expression or even something more implicit, such as 'WHERE w is the solution of ... some other equations.
This is because, contrary to what beginners tend to believe there is no virtue in complication, on the contrary. So they, the mathematicians and math users, use all this where, where, where to enable focussing the essentials of an argument.
Thus you might have seen easier the essentials - and the factorisations - if you had posed the problem as
Differentiate y = p3q6 where...
or better y = (pq2)3. where...
I leave you to fill in and use the ...
Last edited:
epenguin
Science Advisor
- 3,637
- 1,013
This is calculus, not precalculus. 

Mark44
Mentor
- 38,039
- 10,522
What the OP is stuck on is not the actual differentiation, but the factoring, so I did not move this thread.epenguin said:This is calculus, not precalculus.
Last edited:
epenguin
Science Advisor
- 3,637
- 1,013
OK and now I think of it some of the more difficult bits of calculus are really algebraic problems.
Similar threads
- Replies
- 14
- Views
- 3K
- Replies
- 3
- Views
- 1K
- Replies
- 9
- Views
- 2K
- Replies
- 36
- Views
- 4K
- Replies
- 5
- Views
- 4K
- Replies
- 4
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
-
What does this equation mean?
- Started by inuka00123
- Replies: 12
- Precalculus Mathematics Homework Help
-
Finding polar equation of a shifted cricle
- Started by farfromdaijoubu
- Replies: 6
- Precalculus Mathematics Homework Help
-
Intersection of a circle and a sine curve
- Started by vcsharp2003
- Replies: 26
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
