nuclearfireball_42
- 9
- 2
- Homework Statement
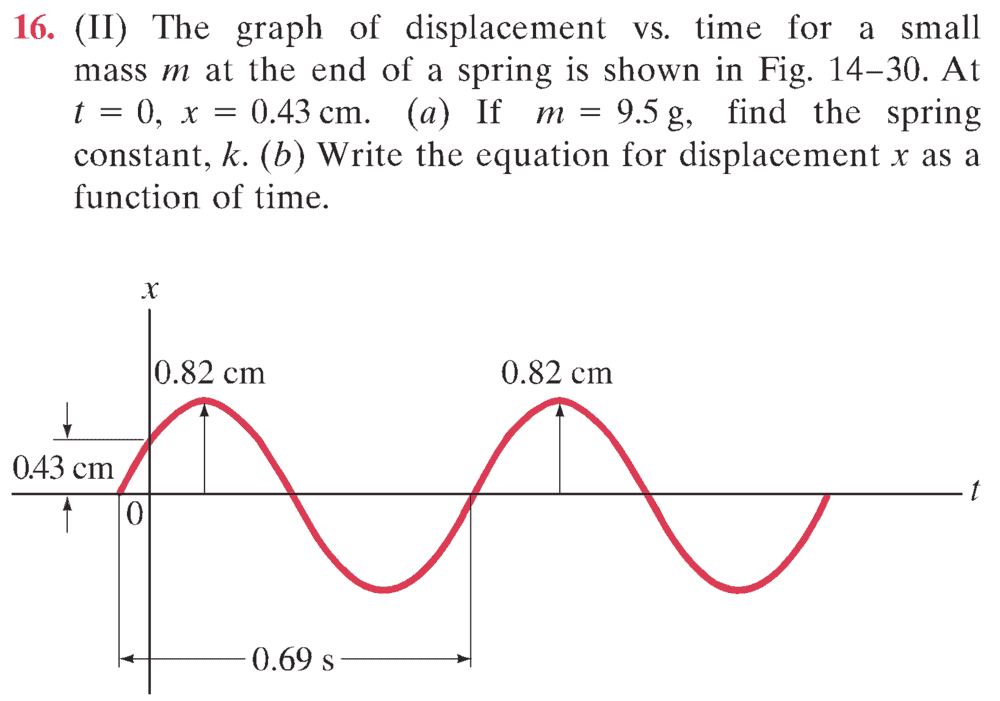
- The graph of displacement vs time for a small mass m at the end of a spring is shown in Fig. 14-30. At t = 0, x = 0.43 cm.
(a) If m = 9.5 g, find the spring constant, k.
(b) Write the equation for displacement x as a function of time.
- Relevant Equations
- x(t) = Asin(ωt + φ)
x(t) = Acos(ωt - φ)
I've got the answer for (a). It's k = 0.78 N/m.
I'm having problems with (b). I know that the equation of displacement in this case should either be :
x(t) = Asin(ωt + φ)
or
x(t) = Acos(ωt - φ)
where A = amplitudeFrom what I understand, both the equation above should give the same result as the sine and cosine functions are the reason for the different signs before the phase angle. But the author of the book wrote the second equation (the one with the cos function) to be the answer. Thinking that my answer which is in the form of the first equation could just be an alternative of the second, I checked the result of the functions numerically and I found them to be different . Is it something to do with my calculation or is my understanding just wrong?
The picture of the graph :
I'm having problems with (b). I know that the equation of displacement in this case should either be :
x(t) = Asin(ωt + φ)
or
x(t) = Acos(ωt - φ)
where A = amplitudeFrom what I understand, both the equation above should give the same result as the sine and cosine functions are the reason for the different signs before the phase angle. But the author of the book wrote the second equation (the one with the cos function) to be the answer. Thinking that my answer which is in the form of the first equation could just be an alternative of the second, I checked the result of the functions numerically and I found them to be different . Is it something to do with my calculation or is my understanding just wrong?
The picture of the graph :