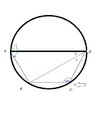
Can Thales' Theorem Help Me Solve My Trapezoid Equation?
- Context: MHB
- Thread starter lornick
- Start date
-
- Tags
- Trapezoid
Click For Summary
SUMMARY
The discussion centers on solving angle calculations in a cyclic trapezoid using Thales' theorem. The user has determined the angles A, B, C, and D as 70°, 110°, 120°, and 60° respectively. It is established that angles E and F must sum to 60° due to the properties of cyclic quadrilaterals. The user realizes that the confusion arose from misinterpreting the angles as acute and obtuse, while Thales' theorem clarifies the relationship between these angles.
PREREQUISITES- Understanding of cyclic quadrilaterals
- Knowledge of Thales' theorem
- Basic angle calculations in geometry
- Familiarity with isosceles trapezoids
- Study the properties of cyclic quadrilaterals
- Learn how to apply Thales' theorem in various geometric contexts
- Explore angle relationships in isosceles trapezoids
- Practice solving problems involving angle calculations in trapezoids
Students studying geometry, mathematics educators, and anyone interested in solving geometric problems involving trapezoids and cyclic figures.
Similar threads
- · Replies 0 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 6 ·
Graduate
Volterra equation of the second kind
- · Replies 1 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 2 ·
High School
Can you read my English on 4 colour theorem?
- · Replies 8 ·